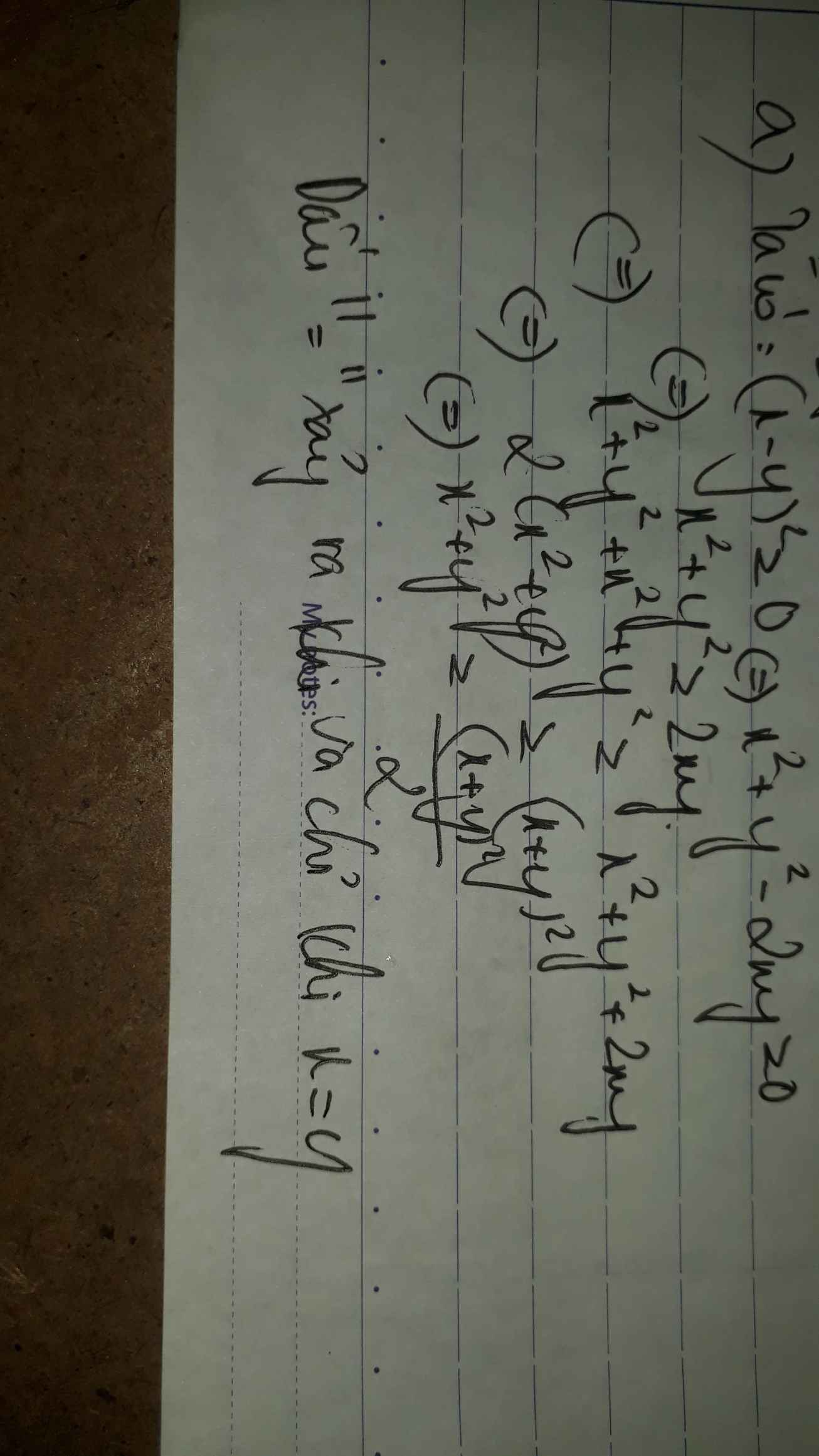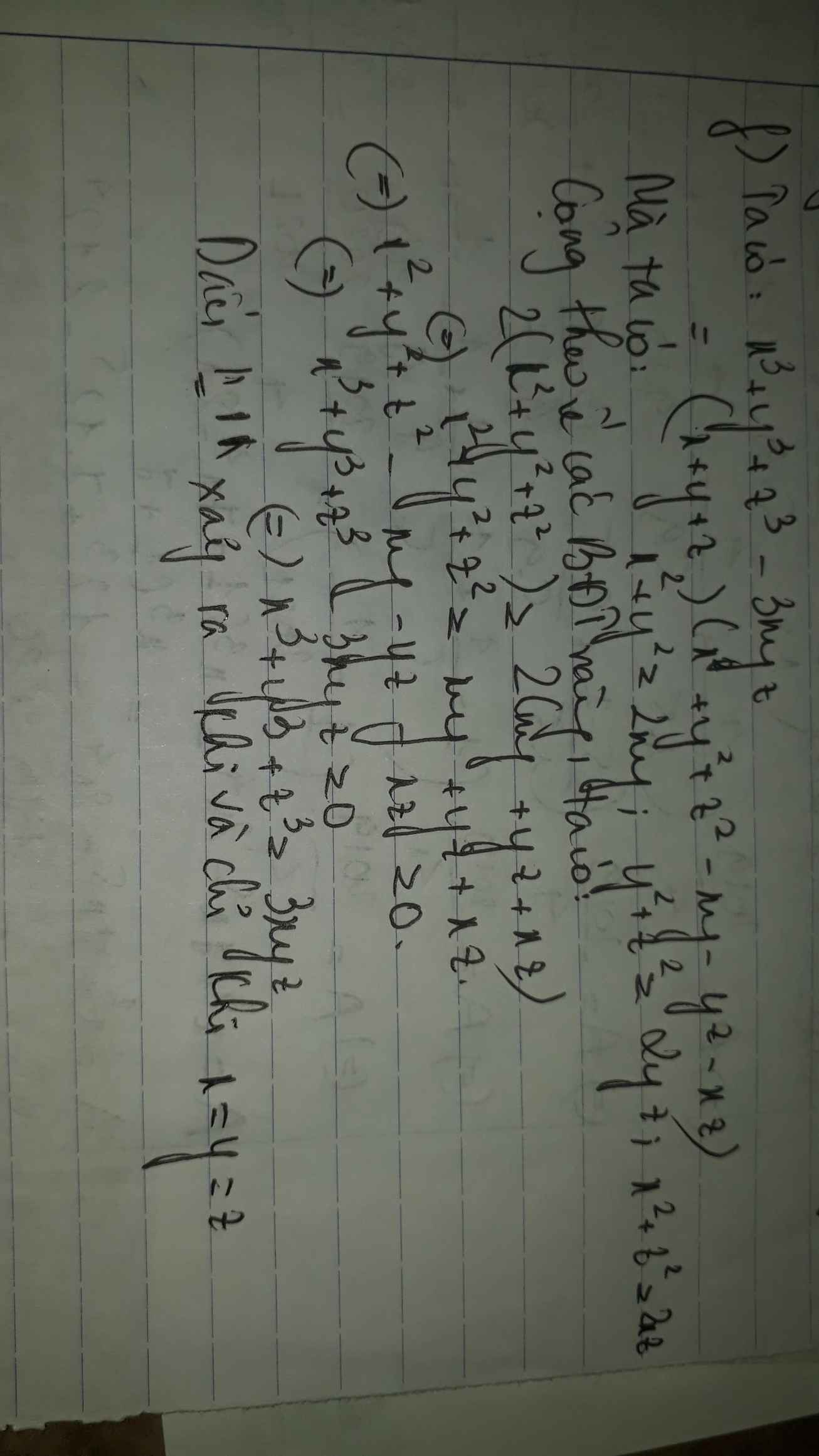a) \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Leftrightarrow2x^2+2y^2\ge\left(x+y\right)^2\Leftrightarrow x^2+y^2\ge2xy\)
\(\Leftrightarrow x^2-2xy+y^2\ge0\Leftrightarrow\left(x-y\right)^2\ge0\left(đúng\right)\)
b) \(x^3+y^3\ge\dfrac{\left(x+y\right)^3}{4}\)
\(\Leftrightarrow4x^3+4y^3\ge\left(x+y\right)^3\Leftrightarrow3x^3+3y^3\ge3x^2y+3xy^2\)
\(\Leftrightarrow3x^2\left(x-y\right)-3y^2\left(x-y\right)\ge0\)
\(\Leftrightarrow3\left(x-y\right)\left(x^2-y^2\right)\ge0\Leftrightarrow3\left(x-y\right)^2\left(x+y\right)\ge0\left(đúng\right)\)
a: Ta có: \(x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Leftrightarrow2x^2+2y^2-x^2-2xy-y^2\ge0\)
\(\Leftrightarrow x^2-2xy+y^2\ge0\)
\(\Leftrightarrow\left(x-y\right)^2\ge0\)(luôn đúng)
c. Áp dụng kết quả phần a ta có:
$x^4+y^4\geq \frac{(x^2+y^2)^2}{2}$
$x^2+y^2\geq \frac{(x+y)^2}{2}$
$\Rightarrow x^4+y^4\geq \frac{1}{2}[\frac{(x+y)^2}{2}]^2=\frac{(x+y)^4}{8}$
Ta có đpcm.
Dấu "=" xảy ra khi $x=y$
e.
BĐT $\Leftrightarrow 3(x^2+y^2+z^2)\geq (x+y+z)^2$
$\Leftrightarrow 2(x^2+y^2+z^2)-2(xy+yz+xz)\geq 0$
$\Leftrightarrow (x-y)^2+(y-z)^2+(z-x)^2\geq 0$ (luôn đúng với mọi $x,y,z>0$
Do đó ta có đpcm.
Dấu "=" xảy ra khi $x=y=z$