a2+b2+1>= ab+a+b <=> a2+b2+1-ab-a-b>=0
<=> 2a2+2b2+2-2ab-2a-2b>=0
<=> (a2-2ab+b2)+(a2-2a+1)+(b2-2b+1)
<=> (a-b)2+(a-1)2+(b-1)2>=0 ( Bất Đẳng Thức luôn đúng)
Vậy a2+b2+1>= ab+a+b
a2+b2+1>= ab+a+b <=> a2+b2+1-ab-a-b>=0
<=> 2a2+2b2+2-2ab-2a-2b>=0
<=> (a2-2ab+b2)+(a2-2a+1)+(b2-2b+1)
<=> (a-b)2+(a-1)2+(b-1)2>=0 ( Bất Đẳng Thức luôn đúng)
Vậy a2+b2+1>= ab+a+b
1 Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
2 Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
3 Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Cho a, b, c thuộc R và a2 + b2 + c2 <= 2. Tìm GTNN P = 2021ca - ab - bc
Cho hai số thực dương a và b thỏa mãn a + b ≤ 2.
Chứng minh a2/a2 + b2/b2 + a ≤ 1
Cho a ≥ 1348, b ≥ 1348. Chứng minh rằng: a2 +b2 +ab ≥ 2022(a + b).
cho a,b là các số hữu tỷ thỏa mãn: (a2+b2-2)(a+b)2+(1-ab)2= -4ab
chứng minh \(\sqrt{1+ab}\) là số hữu tỷ
Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
Chứng minh : (ac + bd)2 + (ad – bc)2 = (a2 + b2)(c2 + d2)
Cho a, b, c là các số dương. Chứng minh : a3 + b3 + abc ≥ ab(a + b + c)
Mn giúp mik vs ;-;
Cho a, b,c là độ dài ba cạnh tam giác. Chứng minh rằng: a/(a2 + bc) + 1/(b2+ ac) + s/(c2+ab) <= (a+b+c)/2abc
1/ a) Chứng minh : (ac + bd)2 + (ad – bc)2 = (a2 + b2)(c2 + d2)
b) Chứng minh bất dẳng thức Bunhiacôpxki : (ac + bd)2 ≤ (a2 + b2)(c2 + d2)
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].
Câu 32. Tìm giá trị lớn nhất của biểu thức: ![]()
Câu 33. Tìm giá trị nhỏ nhất của: ![]() với x, y, z > 0.
với x, y, z > 0.
Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:
a) ab và a/b là số vô tỉ.
b) a + b và a/b là số hữu tỉ (a + b ≠ 0)
c) a + b, a2 và b2 là số hữu tỉ (a + b ≠ 0)
Câu 37. Cho a, b, c > 0. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 38. Cho a, b, c, d > 0. Chứng minh:
![]()
Câu 39. Chứng minh rằng [2x] bằng 2[x] hoặc 2[x] + 1
Câu 40. Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Câu 41. Tìm các giá trị của x để các biểu thức sau có nghĩa:
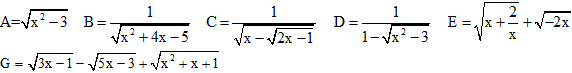 Mn giúp em với ;-;
Mn giúp em với ;-;
cho a,b là số hưu tỉ thỏa man: a2+b2=4-\(\left(\dfrac{ab+2}{a+b}\right)^2\)
Chứng minh \(\sqrt{ab+2}\)ϵQ