\(R=2:2:3.14=\dfrac{1}{3.14}=\dfrac{50}{157}\left(dm\right)\)
=>\(m_A=3\cdot\dfrac{50}{157}=\dfrac{150}{157}\left(dm\right)\)
=>\(a=\dfrac{150}{157}\cdot\dfrac{2}{\sqrt{3}}\simeq1.103\left(dm\right)\)
C=1,103*3=3,309dm
\(R=2:2:3.14=\dfrac{1}{3.14}=\dfrac{50}{157}\left(dm\right)\)
=>\(m_A=3\cdot\dfrac{50}{157}=\dfrac{150}{157}\left(dm\right)\)
=>\(a=\dfrac{150}{157}\cdot\dfrac{2}{\sqrt{3}}\simeq1.103\left(dm\right)\)
C=1,103*3=3,309dm
Tính chu vi và diện tích hìn tròn nội tiếp tam giác đều có cạnh a=12,46
Tính chu vi hình tròn ngoại tiếp tam giác đều có cạnh a = 4.6872.
Cho tam giác đều ABC nội tiếp (O;R). M là điểm trên nửa đường tròn. Xác định M để:
a) Diện tích tam giác MAB lớn nhất;
b) Chu vi tam giác MAB lớn nhất.
Cho ΔABC với góc A = 60 độ, bán kính đường tròn ngoại tiếp bằng 7/√3 và bán kính đường tròn nội tiếp là √3. Tính diện tích và chu vi của Δ
cho biết kết quả
Diện tích của tam giác là 10√3
Chu vi của tam giác là 20
Giúp mình với TT^TT
Cho tam giác ABC đều nội tiếp đường tròn (O; R). Gọi I là một điểm bất kỳ nằm trong tam giác ABC. Các tia AI, BI, CI cắt đường tròn (O) lần lượt tại M, N, P. Tìm vị trí điểm I sao cho chu vi lục giác APBMCN lớn nhất.
Các tam giác trong hai hình quả tim dưới đây đều là tam giác đều .Biết AB=CD=8cm.Tính chu vi của mỗi hình quả tim
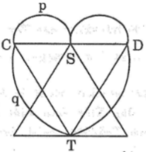
Các tam giác trong hai hình quả tim dưới đây đều là tam giác đều .Biết AB=CD=8cm.Tính chu vi của mỗi hình quả tim
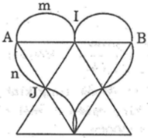
Chứng minh rằng nếu tam giác ABC có chu vi 2p, bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức : S = p.r