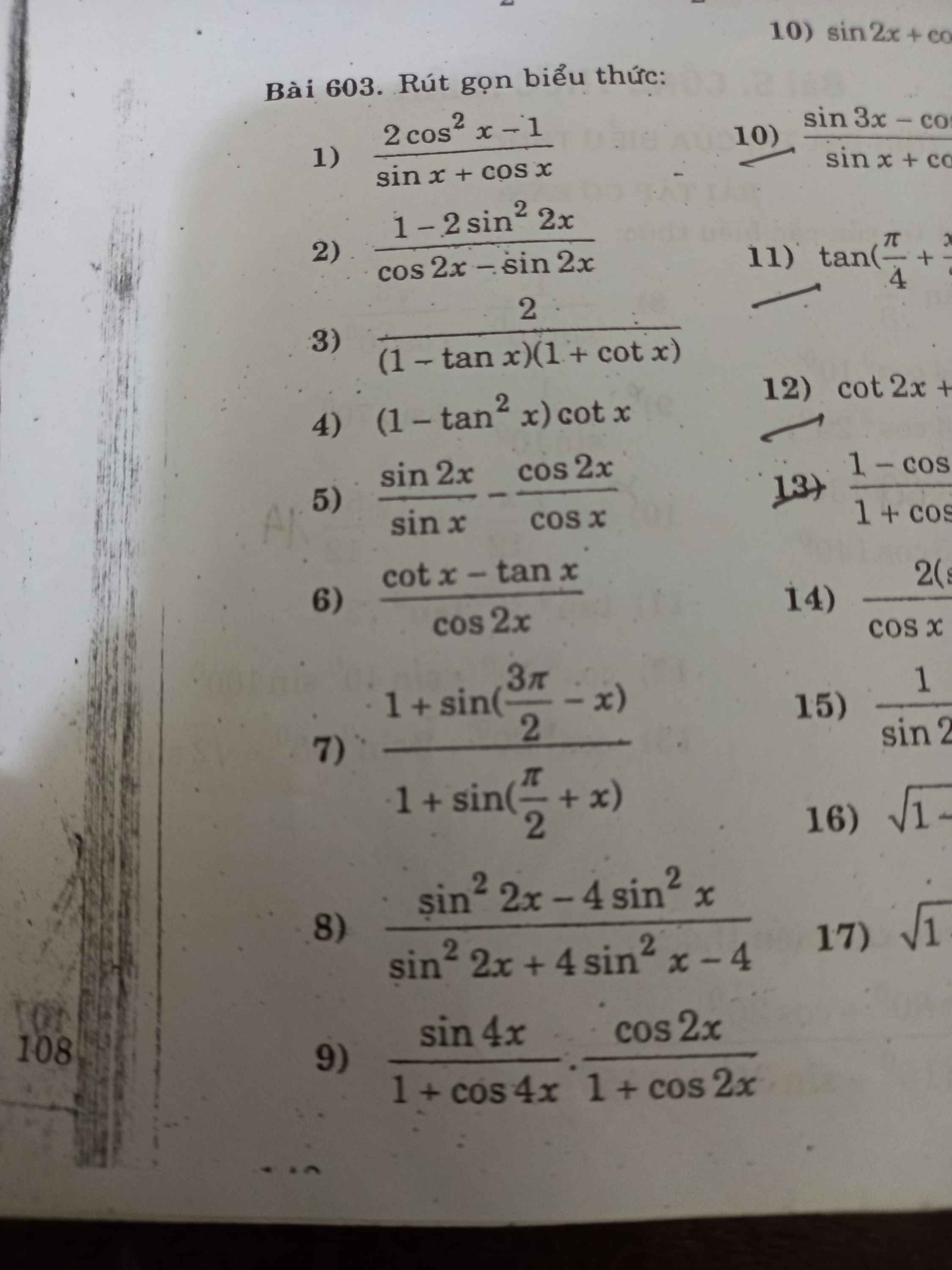Đặt (P): F(x)=ax^2+bx+c
Vì (P) đi qua (0;-3); (5;2); đỉnh là (2;-7) nên ta có hệ:
\(\left\{{}\begin{matrix}a\cdot0^2+b\cdot0+c=-3\\25a+5b+c=2\\\left\{{}\begin{matrix}\dfrac{-b}{2a}=2\\-\dfrac{b^2-4ac}{4a}=-7\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}c=-3\\25a+5b=5\\b=-4a\\b^2-4ac=28a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=-3\\a=1\\b=-4\end{matrix}\right.\)
=>(P): F(x)=x^2-4x-3
Đặt (H): G(x)=ax^2+bx+c
G(x) đi qua (3;0); (-1;0); đỉnh là I(1;4)
=>Hệ pt:
\(\Leftrightarrow\left\{{}\begin{matrix}a\cdot3^2+b\cdot3+c=0\\a\cdot\left(-1\right)^2+b\cdot\left(-1\right)+c=0\\\dfrac{-b}{2a}=1\\-\dfrac{b^2-4ac}{4a}=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}9a+3b+c=0\\a-b+c=0\\b=-2a\\\dfrac{b^2-4ac}{4a}=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8a+4b=0\\b+2a=0\\a-b+c=0\\b^2-4ac=-16a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\a+2a+c=0\\b^2-4ac=-16a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\c=-3a\\\left(-2a\right)^2-4a\cdot\left(-3a\right)=-16a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4a^2+12a+16a=0\\b=-2a\\c=-3a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-7\\b=14\\c=21\end{matrix}\right.\)
=>(H): G(x)=49x^2+14x+21
F(x): x^2-4x-3
=>Ko có câu nào đúng
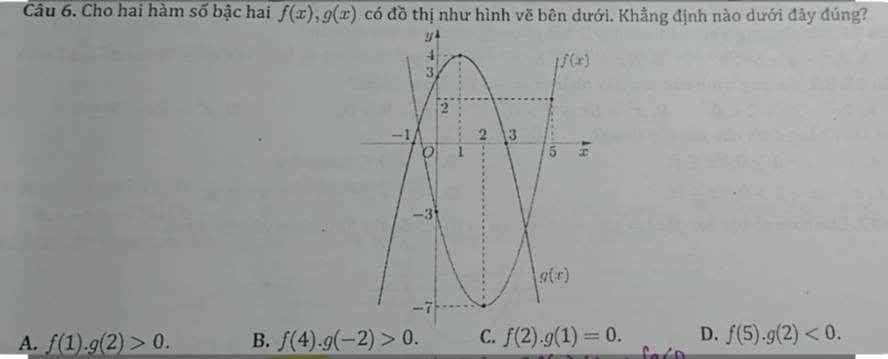





 Lời giải chi tiết đc hôk ạ
Lời giải chi tiết đc hôk ạ