Đáp án A
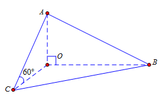
Theo giả thiết OA, OB, OC đôi một vuông góc với nhau nên O A ⊥ O B C , O C là hình chiếu của AC lên mặt phẳng O B C . Do đó, A C O ^ = 60 ° , O A là chiều cao của tứ diện OABC. Xét tam giác vuông AOC có tan 60 ° = O A O C với O A = a ⇒ O C = O A tan 60 ° = a 3 = a 3 3 ; O B = 2 a
Ta có S O B C = 1 2 O B . O C = 1 2 2 a . a 3 3 ; V O A B C = 1 3 O A . S O B C = 1 3 a . a 2 3 3 = a 3 3 9
Cho tứ diện OABC biết OA, OB, OC đôi một vuông góc với nhau, biết O A = 3 , O B = 4 và thể tích khối tứ diện OABC bằng 6. Khi đó khoảng cách từ O đến mặt phẳng (ABC) bằng:
A. 3
B. 41 12
C. 144 41
D. 12 41
Tứ diện OABC, có OA=a, OB=b, OC=c và đôi một vuông góc với nhau. Thể tích khối tứ diện bằng
A. a b c 3
B. abc
C. a b c 6
D. a b c 2
Cho tứ diện OABC có ba cạnh OA;OB;OC đôi một vuông góc với nhau, O A = a 2 2 , O B = O C = a . Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC)Tính thể tích khối tứ diện OABH
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và O A = a , O B = 2 a , O C = 3 a . Thể tích của khối tứ diện OABC bằng
A. V = 2 a 3 3
B. V = a 3 3
C. V = 2 a 3
D. V = a 3
Cho tứ diện OABC có OA;OB;OC đôi một vuông góc và O A = a , O B = b , O C = c . Tính thể tích khối tứ diện OABC.
A. abc
B. abc/3
C. abc/6
D. abc/2
Thể tích của khối tứ diện OABC có O A = O B = O C = a và O A , O B , O C đôi một tạo với nhau một góc 60 ° bằng
A. a 3 6
B. a 3 3
C. 2 a 3 12
D. 2 a 3 4
Thể tích của khối tứ diện OABC có OA=OB=OC=a và OA,OB,OC đôi một tạo với nhau một góc 60 ° bằng
A. a 3 6
B. a 3 3
C. a 3 2 12
D. 2 a 3 4
Cho tứ diện OABC có OA=a; OB=2a; OC=3a đôi một vuông góc với nhau tại O. Lấy M là trung điểm của cạnh AC; N nằm trên cạnh CB sao cho CN=2/3 CB. Tính theo a thể tích khối chóp OAMNB
A. 2 a 3
B. a 3 6
C. 2 a 3 3
D. a 3 3
Cho tứ diện OABC có OA,OB,OC đôi một tạo với nhau góc và OA=OB=a,OC=2a. Côsin góc giữa đường thẳng OC và mặt phẳng (ABC) bằng
A. 5 3
B. 1 3
C. 2 3
D. 2 3 3
