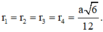Chọn đáp án B
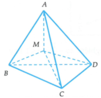
Gọi r1, r2, r3, r4 lần lượt là khoảng cách từ điểm M đến các mặt phẳng (BCD), (ACD), (ABD), (ABC)
Gọi S là diện tích một mặt của tứ diện đều thì
Thể tích tứ diện đều ABCD là V A B C D = a 3 2 12
Ta có V A B C D = V M . B C D + V M . A C D + V M . A B D + V M . A B C
![]()
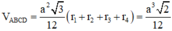
Áp dụng bất đẳng thức Cauchy cho các số dương ta có:
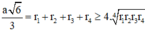
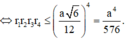
Dấu “=” xảy ra khi và chỉ khi