Đáp án A
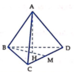
Gọi H là hình chiếu của điểm A trên mặt phẳng(BCD). Do ABCD là tứ diện đều nên tâm H là tâm đường trong ngoại tiếp Δ B C D .
Đặt cạnh của tứ diện là a. Gọi M là trung điểm của CD.
Do Δ B C D đều nên
B M = a 3 2 ⇒ B H = 2 3 B M = 2 3 . a 3 2 = a 3 3
Ta có Δ A B H vuông tại H nên
A H = A B 2 − B H 2 = a 2 − a 3 3 2 = a 6 3
Từ giả thiết ta có
A H = a 6 3 = 6 ⇔ a = 3 6 ⇒ S Δ B C D = a 2 3 4 = 27 3 2
(đvdt).
Vậy thể tích của tứ diện ABCD là
A H = a 6 3 = 6 ⇔ a = 3 6 ⇒ S Δ B C D = a 2 3 4 = 27 3 2
(đvtt).

