Các câu hỏi tương tự
Cho tứ diện ABCD. Gọi P và Q lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AC và BD lần lượt ta lấy các điểm M, N sao cho
A
M
A
C
B
N
B
D
k
(
k
0
)
Chứng minh rằng ba vectơ ...
Đọc tiếp
Cho tứ diện ABCD. Gọi P và Q lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AC và BD lần lượt ta lấy các điểm M, N sao cho
A M A C = B N B D = k ( k > 0 )
Chứng minh rằng ba vectơ P Q → , P M → , P N → đồng phẳng.
Cho tứ diện ABCD. Trên ba cạnh AB, AC, AD lần lượt lấy các điểm B, C, D sao cho đường thẳng BCcắt đường thẳng BC tại K, đường thẳng CD cắt đường thẳng CD tại J, đường thẳng DB cắt đường thẳng DB tại I.a) Chứng minh ba điểm I, J, K thẳng hàng.b) Lấy điểm M ở giữa đoạn thẳng BD; điểm N ở giữa đoạn thẳng CD sao cho đường thẳng MN cắt đường thẳng BC và điểm F nằm bên trong tam giác ABC. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MNF).
Đọc tiếp
Cho tứ diện ABCD. Trên ba cạnh AB, AC, AD lần lượt lấy các điểm B', C', D' sao cho đường thẳng B'C'cắt đường thẳng BC tại K, đường thẳng C'D' cắt đường thẳng CD tại J, đường thẳng D'B' cắt đường thẳng DB tại I.
a) Chứng minh ba điểm I, J, K thẳng hàng.
b) Lấy điểm M ở giữa đoạn thẳng BD; điểm N ở giữa đoạn thẳng CD sao cho đường thẳng MN cắt đường thẳng BC và điểm F nằm bên trong tam giác ABC. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MNF).
Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC. Lấy điểm K thuộc đoạn BD (K không là trung điểm của BD). Tìm giao điểm của đường thẳng AD và mặt phẳng (MNK).
Mn giúp mk câu này vs Trong mặt phẳng Oxy cho các điểm M(0;2) ; N(5;-3) ; P(-2;-2) ; Q(2;-4) lần lượt thuộc các cạnh AB BC CD DA của hình vuông ABCD . Diện tích hình vuông ABCD Đáp án S=10,S=2 mà k hổng bt cách tính mong các b giải giúp sớm Thanks
Cho tứ diện ABCD. Gọi K là điểm thuộc cạnh CD sao cho 2KD3KC và I là điểm thuộc đoạn thẳng BK sao cho IK2IB. Mặt phẳng left(alpharight) đi qua I và luôn cắt các tia AB, AC, AD lần lượt tại các điểm M, N, P (khác đỉnh A). Tìm giá trị nhỏ nhất của biểu thức:
T4.dfrac{AB^2}{AM^2}+9.dfrac{AC^2}{AN^2}+16.dfrac{AD^2}{AP^2}
Đọc tiếp
Cho tứ diện ABCD. Gọi K là điểm thuộc cạnh CD sao cho \(2KD=3KC\) và I là điểm thuộc đoạn thẳng BK sao cho \(IK=2IB\). Mặt phẳng \(\left(\alpha\right)\) đi qua I và luôn cắt các tia AB, AC, AD lần lượt tại các điểm M, N, P (khác đỉnh A). Tìm giá trị nhỏ nhất của biểu thức:
\(T=4.\dfrac{AB^2}{AM^2}+9.\dfrac{AC^2}{AN^2}+16.\dfrac{AD^2}{AP^2}\)
Cho hình thang ABCD có AB // CD và AB 2a, BC CD DA a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.b) Gọi O là trung điểm của AB, O là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO ⊥ (SBC).c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.d) Tìm một điểm cách đ...
Đọc tiếp
Cho hình thang ABCD có AB // CD và AB = 2a, BC = CD = DA = a. Đường thẳng d vuông góc với mặt phẳng (ABCD) tại A. Gọi S là một điểm duy nhất thay đổi trên d. (P) là một mặt phẳng qua A vuông góc với SB tại I và cắt SC, SD lần lượt tại J, K.
a) Chứng minh tứ giác BCJI, AIJK là các tứ giác nội tiếp.
b) Gọi O là trung điểm của AB, O' là tâm đường tròn ngoại tiếp tứ giác BCJI. Chứng minh rằng OO' ⊥ (SBC).
c) Chứng minh rằng khi S thay đổi trên d thì JK luôn luôn đi qua một điểm cố định.
d) Tìm một điểm cách đều các điểm A, B, C, D, I, J, K và tìm khoảng cách đó.
e) Gọi M là giao điểm của JK và (ABCD). Chứng minh rằng AM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.
f) Khi S thay đổi trên d, các điểm I, J, K lần lượt chạy trên đường nào.
Cho tứ diện ABCD và điểm M thuộc miền trong của tam giác ACD. Gọi I và J lần lượt là 2 điểm trên cạnh BC và BD sao cho IJ không song song với CD. Gọi H và K lần lượt là giao điểm của IJ và CD; MH và AC. giao tuyến của 2 mặt phẳng (ACD) và (IJM) là
A. KI
B. KJ
C. MI
D. MH
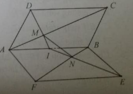
Hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Trên cạnh AC lấy điểm M và trên cạnh BF lấy điểm N sao cho AM/AC = BN/BF = k. Tìm k để MN // DE.
A. k = 1/3
B. k = 3
C. k = 1/2
D. k = 2
Cho tứ diện ABCD. Trên cạnh AB lấy điểm I và lấy các điểm J, K lần lượt là điểm thuộc miền trong các tam giác BCD và ACD. Gọi L là giao điểm của JK với mặt phẳng (ABC)
a) Hãy xác định điểm L.
b) Tìm giao tuyến của mặt phẳng (IJK) với các mặt của tứ diện ABCD.