Các câu hỏi tương tự
Cho tứ diện ABCD. Lấy các điểm M, N, P, Q lần lượt thuộc AB, BC, CD, DA sao cho
A
M
→
1
3
A
B
→
,
B
N
→
2
3
B
C
→
,...
Đọc tiếp
Cho tứ diện ABCD. Lấy các điểm M, N, P, Q lần lượt thuộc AB, BC, CD, DA sao cho A M → = 1 3 A B → , B N → = 2 3 B C → , A Q → = 1 2 A D → và D P → = k D C → . Tìm k để bôn điểm P, Q, M, N cùng nằm trên một mặt phẳng.
A. k = − 2
B. k = 1 2
C. k = − 1 2
D. k = 2
Cho bốn điểm A,B,C,D không cùng nằm trong một mặt phẳng. Trên AB,AD lần lượt lấy các điểm M và N sao cho MN cắt BD tại I. Điểm I không thuộc mặt phẳng nào sau đây:
A. (ACD)
B. (CMN)
C. (BCD)
D. (ABD)
Cho khối tứ diện ABCD. Lấy điểm M nằm giữa A và B, điểm N nằm giữa C và D. Bằng hai mặt phẳng (CDM) và (ABN), ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây ? A. MANC, BCDN, AMND, ABND. B. MANC, BCMN, AMND, MBND. C. ABCN, ABND, AMND, MBND. D. NACB, BCMN, ABND, MBND.
Đọc tiếp
Cho khối tứ diện ABCD. Lấy điểm M nằm giữa A và B, điểm N nằm giữa C và D. Bằng hai mặt phẳng (CDM) và (ABN), ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây ?
A. MANC, BCDN, AMND, ABND.
B. MANC, BCMN, AMND, MBND.
C. ABCN, ABND, AMND, MBND.
D. NACB, BCMN, ABND, MBND.
câu 1 : Trên nữa mặt phẳng đường tròn (O) đường kính AB ta lấy điểm M bất kỳ ( M khác A và B ), các tiếp tuyến tại M và B với nửa đường tròn cắt nhau ở C . Từ tâm O của nữa đường tròn ta kẻ đường thẳng song song với MB cắt các tiếp tuyến CM và CB lần lượt tại D và E .CM rằng :a) Tam giác CDE cânb) AD là tiếp tuyến của nữa đường tròn c) Khi M di chuyển trên nữa đường tròn thì tích AB . CD không thay đỗicâu 2 :cho các hàm số y2mx+3 và y (n-1)x-2a) biết rằng trên cùng một mặt phẳng tọa độ , dồ thị...
Đọc tiếp
câu 1 :
Trên nữa mặt phẳng đường tròn (O) đường kính AB ta lấy điểm M bất kỳ ( M khác A và B ), các tiếp tuyến tại M và B với nửa đường tròn cắt nhau ở C . Từ tâm O của nữa đường tròn ta kẻ đường thẳng song song với MB cắt các tiếp tuyến CM và CB lần lượt tại D và E .CM rằng :
a) Tam giác CDE cân
b) AD là tiếp tuyến của nữa đường tròn
c) Khi M di chuyển trên nữa đường tròn thì tích AB . CD không thay đỗi
câu 2 :
cho các hàm số y=2mx+3 và y = (n-1)x-2
a) biết rằng trên cùng một mặt phẳng tọa độ , dồ thị các hàm số này cắt nhau tại điểm A ( 1;-1). Hãy xác định m và n
b) Với các giá trị của m và n tìm được ở trên , hãy vẽ đồi thị của các hàm số tương ứng trên cùng một mặt phẳng tọa độ
Cho tứ diện S.ABC có M, N lần lượt là điểm chia SA và SC theo cùng tỉ số k. Mặt phẳng (a) qua MN cắt ( ABC ) theo giao tuyến cắt BC tại P và cắt AB tại Q. Tính tỉ số
Q
B
Q
A
để MNPQ là hình bình hành. A. k B. 2k C.
1
2
k
D.
3
2
k
Đọc tiếp
Cho tứ diện S.ABC có M, N lần lượt là điểm chia SA và SC theo cùng tỉ số k. Mặt phẳng (a) qua MN cắt ( ABC ) theo giao tuyến cắt BC tại P và cắt AB tại Q. Tính tỉ số Q B Q A để MNPQ là hình bình hành.
A. k
B. 2k
C. 1 2 k
D. 3 2 k
1, Cho tg ABC có A90 . Gọi I là TĐ của cạnh AC . Trên tia đối của tia IB lấy điểm D/ IBID. Nối C với D a, CMR tg AIB tg CID b, Gọi M là Tđ Của BC, N là TĐ của AD CMR I là TĐ cuar MN c, Cmr góc AIBBIC Tìm đk tg ABC để AC vuông CD2, Cho tam giác ABC gọi M là TĐ của cạnh BC . Trên tia đối của MA lấy điểm E sao cho MEMA CMR: a,ACBE và AD // BE b, Gọi I là 1 điểm của bk AC, Gọi K là 1 điểm trên BE / AIEK. CMR 3 điểm I,M,K thẳng hàng c, Từ EH vg BC tại H biết HBE50 MEB25 Tính HEM và BME
Đọc tiếp
1, Cho tg ABC có A<90 . Gọi I là TĐ của cạnh AC . Trên tia đối của tia IB lấy điểm D/ IB=ID. Nối C với D a, CMR tg AIB= tg CID b, Gọi M là Tđ Của BC, N là TĐ của AD CMR I là TĐ cuar MN c, Cmr góc AIB<BIC Tìm đk tg ABC để AC vuông CD
2, Cho tam giác ABC gọi M là TĐ của cạnh BC . Trên tia đối của MA lấy điểm E sao cho ME=MA CMR: a,AC=BE và AD // BE b, Gọi I là 1 điểm của bk AC, Gọi K là 1 điểm trên BE / AI=EK. CMR 3 điểm I,M,K thẳng hàng c, Từ EH vg BC tại H biết HBE=50 MEB=25 Tính HEM và BME
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;2;-1),M(2;4;1),N(1;5;3). Tìm toạ độ điểm C nằm trên mặt phẳng (P):x+z-27=0 sao cho tồn tại các điểm B,D tương ứng thuộc các tia AM, AN để tứ giác ABCD là hình thoi.
A. C(6;-17;21).
B. C(20;15;7).
C. C(6;21;21).
D. C(18;-7;9).
Trong không gian Oxyz, cho tứ diện ABCD có A (1;1;1), B (2;0;2), C ( -1;-1;0) và D ( 0;3;4). Trên các cạnh AB , AC, AD lần lượt lấy các điểm B, C, D sao cho thể tích của khối tứ diện ABCD nhỏ nhất và
A
B
A
B
+
A
C
A
C
+
A...
Đọc tiếp
Trong không gian Oxyz, cho tứ diện ABCD có A (1;1;1), B (2;0;2), C ( -1;-1;0) và D ( 0;3;4). Trên các cạnh AB , AC, AD lần lượt lấy các điểm B', C', D' sao cho thể tích của khối tứ diện AB'C'D' nhỏ nhất và A B A B ' + A C A C ' + A D A D ' = 4 . Tìm phương trình của mặt phẳng (B’C’D’)
A. 16 x + 40 y - 44 z + 39 = 0
B. 16 x - 40 y - 44 z + 39 = 0
C. 16 x + 40 y + 44 z + 39 = 0
D. 16 x + 40 y - 44 z - 39 = 0
Cho hình lập phương a 1 có cạnh bằng a 1. Một đường thẳng d đi qua đỉnh D và tâm I cuả mặt bên BCCB. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCCB) và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d ( tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là: A. a 1 B. a
1
2
C.
a
2
5
D.
a...
Đọc tiếp
Cho hình lập phương a = 1 có cạnh bằng a = 1. Một đường thẳng d đi qua đỉnh D ' và tâm I cuả mặt bên BCC'B'. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCC'B') và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d ( tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là:
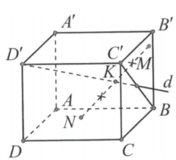
A. a =1
B. a = 1 2
C. a = 2 5
D. a = 1 3



