Question

Cho tứ diện ABCD. Lấy các điểm M, N, P, Q lần lượt thuộc AB, BC, CD, DA sao cho A M → = 1 3 A B → , B N → = 2 3 B C → , A Q → = 1 2 A D →  và D P → = k D C → .  Tìm k để bôn điểm P, Q, M, N cùng nằm trên một mặt phẳng.

A. k = − 2

B. k = 1 2

C. k = − 1 2

D.  k = 2

Answer 1

Đáp án B

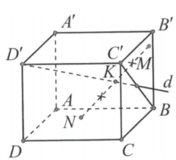
 Ta có  A M → = 1 3 A B → = 1 3 A B → ;

           B N → = 2 3 B C → ⇒ A N → − A B → = 2 3 A C → − 2 3 A B → ⇒ A N → = 1 3 A B → + 2 3 A C →

           A Q → = 1 2 A D →

           D P → = k D C → ⇒ A P → − A D → = k A C → − A D → ⇒ A P → = k A C → + 1 − k A D →

Điều kiện 4 điểm P,Q,M,N đồng phẳng là tồn tại x , y , z ; x + y + z = 1   thỏa mãn

           A P → = x A M → + y A N → + z A Q → ⇔ x + y + z = 1 1 3 x + 1 3 y = 0 2 3 y = k 1 2 z = 1 − k

Từ pt(1) và pt(2) ta có  z = 1 ⇒ k = 1 2