Đáp án A
- Từ giả thiết ta có 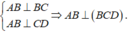
- Do đó 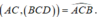
Đáp án A

- Từ giả thiết ta có 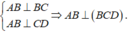
- Do đó 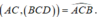
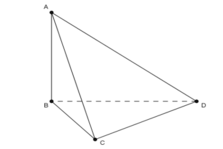
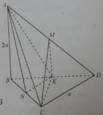
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa AC với mặt phẳng (ABD) bằng:
A. 5
B. 1
C. 51 17
D. Không xác định
cho hình tứ diện ABCD có AB,AC,AD đôi một vuông góc và AB=AC=AD=5cm gọi M là trung điểm BC a) chứng minh BC vuông góc ADM b) tính khoảng cách từ điểm A đén BCD C) tính góc giữa đường thẳng DM và mặt phẳng ABC
Cho tứ diện ABCD với A C = 2 3 A D , ∠ C A B = ∠ D A B = 60 ° , CD=AD .Gọi là góc giữa AB và CD. Chọn khẳng định đúng?
A. cos φ = 1 4
B. φ = 60 °
C. φ = 30 °
D. cos φ = 3 4
Cho tứ diện ABCD với A C = 2 3 A D , ∠ C A B = ∠ D A B = 60 ° , CD=AD .Gọi là góc giữa AB và CD. Chọn khẳng định đúng?
A. cos φ = 1 4
B. φ = 60 °
C. φ = 30 °
D. cos φ = 3 4
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau, biết AB=AC=AD=1. Số đo góc giữa hai đường thẳng AB và CD bằng
A. 45 ⁰ .
B. 60 ° .
C. 30 ⁰ .
D. 90 ⁰ .
Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60 o . Gọi M và N lần lượt là trung điểm của AB và CD.
Góc giữa hai mặt phẳng (ACD) và (BCD) là:
A. A C B ⏜
B. A N B ⏜
C. A D B ⏜
D. M N B ⏜
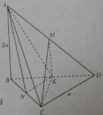
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Gọi M là trung điểm của AD và K là trung điểm của BD
Góc giữa CM với mặt phẳng (BCD) là:
A. B C M ⏜
B. D C M ⏜
C. K C M ⏜
D. A C M ⏜
Cho tứ diện ABCD có BC = CD = BD = 2a, AC = AD = 2 , AB = a. Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là:
A. 90 o .
B. 60 o .
C. 45 o
D. 30 o