Đáp án D
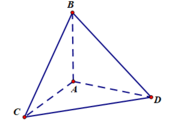
A B ⊥ A C A B ⊥ A D ⇒ A B ⊥ A C D ⇒ A B ⊥ C D ⇒ A B ; C D = 90 0
Đáp án D

A B ⊥ A C A B ⊥ A D ⇒ A B ⊥ A C D ⇒ A B ⊥ C D ⇒ A B ; C D = 90 0
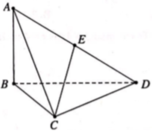
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và A B = a 6 2 ; A C = a 2 ; C D = a Gọi E là trung điểm của AD (tham khảo hình vẽ). Góc giữa hai đường thẳng AB và CE bằng
A. 60 độ
B. 45 độ
C. 30 độ
D. 90 độ
Cho tứ diện ABCD có A B = C D = a , A C = B D = b , A D = B C = c . Gọi α là số đo của góc hợp bởi hai đường thẳng AB, CD. Khi đó cos α bằng
A. b 2 - c 2 a 2
B. b 2 - c 2 2 a 2
C. a 2 2 b 2 + c 2
D. a 2 b 2 + c 2
Cho tứ diện ABCD có A B , A C , A D đôi một vuông góc với nhau, A B = a , A C = b , A D = c . Tính thể tích V của khối tứ diện ABCD theo a, b, c
A. V = a b c 2
B. V = a b c 6
C. V = a b c 3
D. V = a b c
Cho tứ diện ABCD có A C = 1 2 A D , ∠ C A B = 60 ° , ∠ D A B = 120 ° , C D = A D . Góc giữa đường thẳng AB và CD bằng
A. a r c cos 3 4
B. 30 °
C. 60 °
D. a r c cos 1 4
Cho tứ diện ABCD có A B = A C = A D và B A C ^ = B A D ^ = 60 ° . Xác định góc giữa hai đường thẳng AB và CD
A. 90 °
B. 45 °
C. 60 °
D. 30 °
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng A B = a , A C = a 2 , A D = a 3 , a > 0 . Thể tích V của khối tứ diện ABCD là:
A. V = 1 3 a 3 6
B. V = 1 6 a 3 6
C. V = 1 2 a 3 6
D. V = 1 9 a 3 6
Cho tứ diện ABCD với A C = 3 2 A D , C A B ^ = D A B ^ = 60 ° , C D = A D . Gọi φ là góc giữa hai đường thẳng AB và CD. Chọn khẳng định đúng về góc φ
A. φ = 30 °
B . φ = 60 °
C. cos φ = 1 4
D. cos φ = 3 4
Cho tứ diện ABCD có độ dài các cạnh AB=AC=AD=BC=BD=a và C D = a 2 . Góc giữa hai đường thẳng AD và BC bằng
A. 30 °
B. 90 °
C. 45 °
D. 60 °
Cho tứ diện ABCD có cạnh AB,AC,AD đôi một vuông góc. Biết rằng A B = A C = 2 a và góc tạo bởi hai mặt phẳng (DCB) và (ABC) bằng 60 0 . Tính thể tích khối tứ diện ABCD.
A. 2 6 a 3 3
B. 4 6 a 3 3
C. 2 6 a 3
D. 4 6 a 3