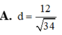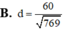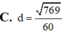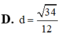Các câu hỏi tương tự
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, AB 6a, AC 7a, AD 8a . Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là: A. 14
a
2
. B. 28
a
2
. C. 42
a
2
. D. 7
a
2...
Đọc tiếp
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, AB = 6a, AC= 7a, AD = 8a . Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là:
A. 14 a 2 .
B. 28 a 2 .
C. 42 a 2 .
D. 7 a 2 .
Cho tứ diện ABCD có ba cặp cạnh đối diện bằng nhau là AB = CD, AC = BD và AD = BC. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh MN ⊥ AB và MN ⊥ CD. Mặt phẳng (CDM) có vuông góc với mặt phẳng (ABN) không? Vì sao?
Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh AB và CD của tứ diện ABCD là đường vuông góc chung của AB và CD thì AC = BD và AD = BC.
Cho tứ diện ABCD có AB = CD = 5 , AC = BD = 10 , AD = BC = 13 . Tính thể tích tứ diện đã cho
A . 5 26
B . 5 26 6
C. 4
D. 2
Cho tứ diện đều ABCD đều có cạnh bằng a
a) tính góc giữa hai đường thẳng AB và CD ,AD và BC
b) tính góc giữa các vectơ AC và AB ,AC VÀ DA
Xem chi tiết
b1: cho hình hộp ABCDA'B'C'D' có tất cả các mặt đều là hinh fthoi cạnh a. góc BAA'= góc BAD = góc DAA' = 60 độ. tính độ dài AC
b2: cho tứ diện ABCD có CD=z/2 AB. I,J,K lần lượt là trung điểm của BC,AC,BD. biết JK=5/6AB. tính góc giữa CD với Ị và AB
Tính khoảng cách giữa hai cạnh AB và CD của hình tứ diện ABCD biết rằng AC = BC = AD = BD = a và AB = p, CD = q.
Cho tứ diện ABCD có BC CD BD 2a, AC AD
2
, AB a. Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là: A.
90
o
. B.
60
o
. C.
45
o
D.
30
o
Đọc tiếp
Cho tứ diện ABCD có BC = CD = BD = 2a, AC = AD = 2 , AB = a. Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là:
A. 90 o .
B. 60 o .
C. 45 o
D. 30 o
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), ACAD4,AB3, BC5 Tính khoảng cách d từ điểm A đến mặt phẳng (BCD).
Đọc tiếp
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC=AD=4,AB=3, BC=5 Tính khoảng cách d từ điểm A đến mặt phẳng (BCD).