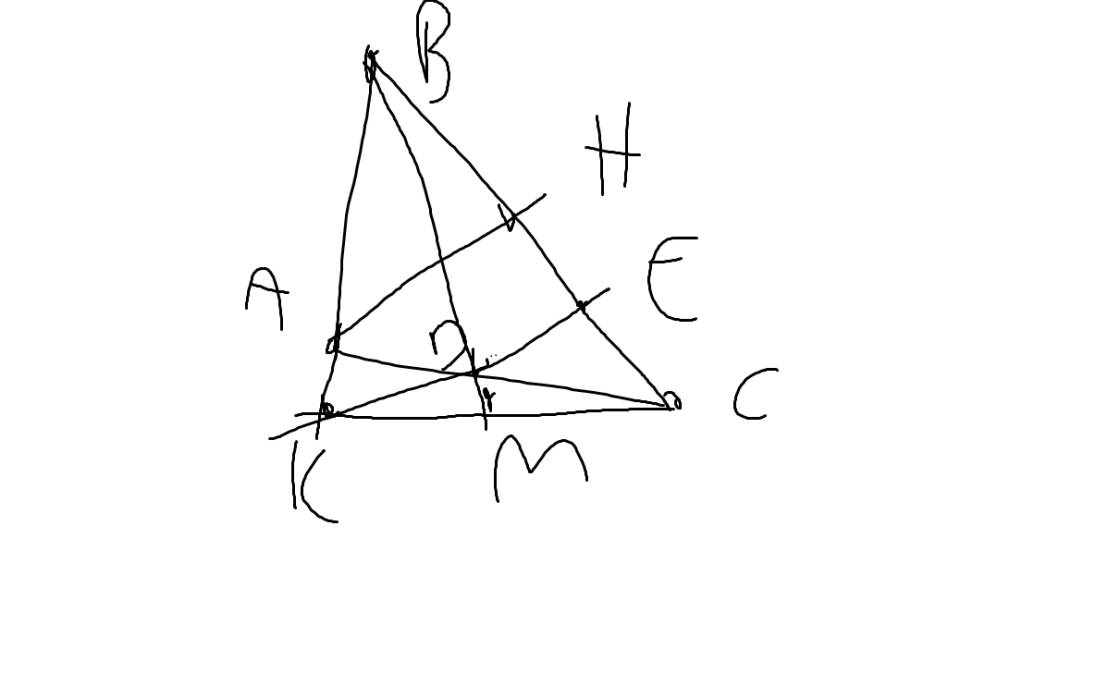Cho tgiac ABC vuông tại A. Trên cạnh BC lấy E sao cho AB = BE. Tia phân giác của B cắt cạnh AC ở D
a) chứng minh tgiac ABD = tgiac EBD
b) chứng minh: BD vuông góc với AE tại trung điểm I của đoạn AE
c) kẻ AH vuông góc với BC, (H thuộc BC) chứng minh AH // DE
d) so sánh ABC = EDC
e) gọi K là giao điểm của ED và BA, M là trung điểm KC. chứng minh B, D, M thẳng hàng
- Ghi GT - KL với vẽ hình đầy đủ giúp tớ với nhaa
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>BA=BE
=>B nằm trên đường trung trực của AE(2)
Ta có: ΔBAD=ΔBED
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE tại trung điểm I của AE
c: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Ta có: AH\(\perp\)BC
DE\(\perp\)BC
Do đó: AH//DE
d: Ta có: \(\widehat{EDC}+\widehat{ACB}=90^0\)(ΔEDC vuông tại E)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{EDC}=\widehat{ABC}\)
e: Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAK=ΔDEC
=>DK=DC và AK=EC
Ta có: BK=BA+AK
BC=BE+EC
mà BA=BE và AK=EC
nên BK=BC
=>B nằm trên đường trung trực của KC(3)
Ta có: DK=DC
=>D nằm trên đường trung trực của KC(4)
Ta có: MK=MC
=>M nằm trên đường trung trực của CK(5)
Từ (3),(4),(5) suy ra B,D,M thẳng hàng