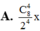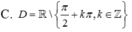Xét số ![]() được lập từ các chữ số thuộc tập A.
được lập từ các chữ số thuộc tập A.
Vì x lẻ nên e ∈ {1; 3; 5; 7} , suy ra có 4 cách chọn e. Bốn chữ số còn lại được chọn từ 7 chữ số của tập A \ {e} nên có cách
Suy ra, có 4.840=3360 số lẻ gồm năm chữ số khác nhau.
Mà số x bắt đầu bằng 123 có số.
Vậy số x thỏa yêu cầu bài toán là :3360- 20=3340 số.
Chọn A.