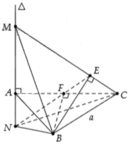
Cho tam giác OAB đều cạnh a. Trên đường thẳng d qua O và vuông góc với mặt phẳng (OAB) lấy điểm M sao cho OM=x. Gọi E, F lần lượt là hình chiếu vuông góc của A trên MB và OB. Gọi N là giao điểm của EF và OM. Tìm x để thể tích tứ diện ABMN có giá trị nhỏ nhất
A. x = a 2 .
B. x = a 2 2 .
C. x = a 6 12 .
D. x = a 3 2 .
Đáp án B

Ta có
A F ⊥ O B , A F ⊥ M O ⇒ A F ⊥ M O B ⇒ A F ⊥ M B
Mà M B ⊥ A E nên M B ⊥ A E F ⇒ M B ⊥ E F .
Suy ra Δ M O B ∽ Δ M E N , mà Δ M E N ∽ Δ F O N nên Δ M O B ∽ Δ F O N . Khi đó O B O M = O N O F ⇒ O N = O B . O F O M = a . a 2 x = a 2 2 x .
Từ
V A B M N = V M . O A B + V N . O A B = 1 3 . S Δ O A B . O M + O N = 1 3 . a 2 3 4 . x + a 2 2 x
⇒ V A B M N = a 2 3 12 x + a 2 2 x ≥ a 2 3 12 .2 x . a 2 2 x = a 2 3 12 . 2 a = a 3 6 12
Dấu “=” xảy ra
⇔ x = a 2 2 x ⇔ 2 x 2 = a 2 ⇔ x = a 2 2 .