Bài 4. Cho tam giác ABC với trực tâm H, trọng tâm G, tâm đường tròn ngoại tiếp O. Gọi M, N lần lượt là trung điểm của BC, AC. Chứng minh rằng tam giác MON đồng dạng AHB. Từ đó chứng minh H, G, O thẳng hàng.Bài 5. Cho tam giác ABC. Dựng ra ngoài các tam giác ABF và ACE lần lượt vuông tại B, C và đồng dạng với nhau. BE giao CF tại K. Chứng minh rằng AK ⊥ BC.Bài 6. Cho tứ giác ABCD có hai đường chéo cắt nhau tại I thỏa mãn tam giác AID đòng dạng tam giác BIC. Kẻ IH ⊥ AD, IK ⊥ BC. M, N lần lượt là t...
Đọc tiếp
Bài 4. Cho tam giác ABC với trực tâm H, trọng tâm G, tâm đường tròn ngoại tiếp O. Gọi M, N lần lượt là trung điểm của BC, AC. Chứng minh rằng tam giác MON đồng dạng AHB. Từ đó chứng minh H, G, O thẳng hàng.
Bài 5. Cho tam giác ABC. Dựng ra ngoài các tam giác ABF và ACE lần lượt vuông tại B, C và đồng dạng với nhau. BE giao CF tại K. Chứng minh rằng AK ⊥ BC.
Bài 6. Cho tứ giác ABCD có hai đường chéo cắt nhau tại I thỏa mãn tam giác AID đòng dạng tam giác BIC. Kẻ IH ⊥ AD, IK ⊥ BC. M, N lần lượt là trung điểm AB, CD. Chứng minh rằng MN ⊥ HK.
Bài 7. Cho tứ giác ABCD có hai đường chéo cắt nhau tại O. Gọi M, N lần lượt là trung điểm AB, CD; H, K lần lượt là trực tâm các tam giác AOD, BOC. Chứng minh rằng MN ⊥ HK.
Bài 8. Cho tam giác ABC. Các đường cao AD, BE, CF . M thuộc tia DF , N thuộc tia DE sao cho ∠M AN = ∠BAC. Chứng minh rằng A là tâm đường tròn bàng tiếp góc D của tam giác DMN .
Bài 9. Cho tứ giác ABCD có hai đường chéo AC = BD. Về phía ngoài tứ giác dựng các tam giác cân đồng dạng AMB và CND (cân tại M, N ). Gọi P, Q lần lượt là trung điểm của AD, BC. Chứng minh rằng M N vuông góc với PQ.
Bài 10. Cho tam giác ABC. Các đường cao AD, BE, CF . Trên AB, AC lấy các điểm K, L sao cho ∠FDK = ∠EDL = 90◦. Gọi M là trung điểm KL. Chứng minh rằng AM ⊥ EF .
Mong các bạn giúp đỡ mình. Giúp được bài nào thì giúp nhé.
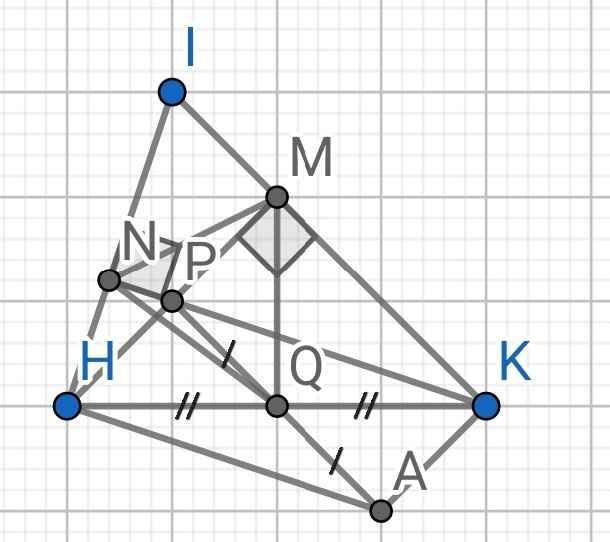 a) Do PQ = QA (gt)
a) Do PQ = QA (gt)


