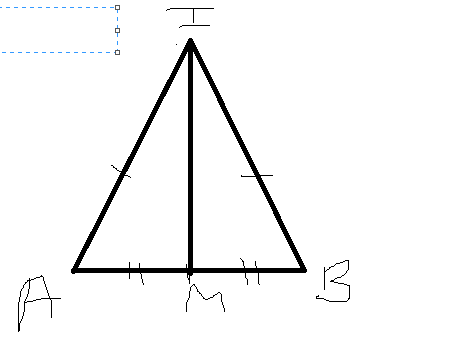
Xét tg IMA và tg IMB có \(IA=IB;AM=MB;IM chung\) nên \(\Delta IMA=\Delta IMB\left(c.c.c\right)\)
Do đó \(\widehat{AIM}=\widehat{BIM}\)
Do đó IM là p/g góc AIB
Ta có: IA = IB (gt) ⇒ ΔIAB là Δ cân \(\Rightarrow\widehat{A}=\widehat{B}\)
Xét ΔIAM và ΔIBM ta có:
IA = IB (gt)
\(\widehat{A}=\widehat{B}\left(cmt\right)\)
AM = BM (M là trung điểm của AB)
⇒ΔIAM=ΔIBM (c.g.c) \(\Rightarrow\widehat{AIM}=\widehat{BIM}\)(2 góc tương ứng) ⇒ IM là đường phần giác của \(\widehat{AIB}\)