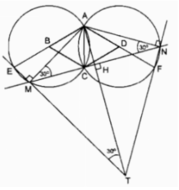
Cho tam giác đều ACB và ACD, cạnh a. Lần lượt lấy B và D làm tâm vẽ hai đường tròn bán kính a. Kẻ các đường kính ABE và ADF. Trên cung nhỏ CE của đường tròn tâm B lấy điểm M (không trùng với E và C). Đường thẳng CM cắt đường tròn tâm D tại điểm thứ hai là N. Hai đường thẳng EM và NF cắt nhau tại điểm T. Gọi H là giao điểm của AT và MN.
Chứng minh:
MNT là tam giác đều.