Các câu hỏi tương tự
Cho tam giác ABC vuông tại A có đường cao AH. Biết BH= 4cm, CH= 9cm. a) Tính AH, AB, AC ? b) Gọi M là trung điểm của AC. Tính góc BMC? (số đo làm tròn đến độ) c) Kẻ AK vuông góc BM tại M. Chứng minh góc ACB = góc BKH
giúp mình với ạ
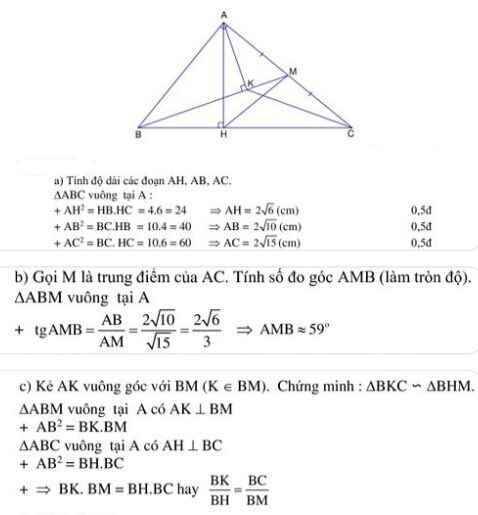
1) Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai đoạn: BH=4cm và HC=6cm
a) Tính độ dài các đoạn AH,AB,AC
b) Gọi M là trung điểm của AC. Tính số đo góc AMB( làm tròn đến độ )
c) Kẻ AK vuông góc với BM (K thuộc BM) . Chứng minh : BK.BM=BH.BC
Vẽ hình luôn ah
Giúp mình 3 bài này với ạ. Xin cảm ơn.Bài 1 : So sánh : 4+sqrt{5}và 8-sqrt{2}Bài 2: Tam giác ABC vuông tại A, đường cao AH, biết BH4cm và HC 6cma) Tính độ dài AH, AB, ACb) Gọi M là trung điểm của AC. Tính số đo góc AMB ( làm tròn đến độ )c) Kẻ AK vuông góc với BM ( K inBM ). Chứng minh rằng Delta BKCđồng dạng với Delta BHMBài 2 giúp mình ý c thôi ạ ^^Bài 3 : Tìm x, biết: ^{x^2+2015x-20142sqrt{2017x-2016}}Mình cần gấp, mong các bạn giúp.
Đọc tiếp
Giúp mình 3 bài này với ạ. Xin cảm ơn.
Bài 1 : So sánh : \(4+\sqrt{5}\)và \(8-\sqrt{2}\)
Bài 2: Tam giác ABC vuông tại A, đường cao AH, biết BH=4cm và HC = 6cm
a) Tính độ dài AH, AB, AC
b) Gọi M là trung điểm của AC. Tính số đo góc AMB ( làm tròn đến độ )
c) Kẻ AK vuông góc với BM ( K \(\in\)BM ). Chứng minh rằng \(\Delta BKC\)đồng dạng với \(\Delta BHM\)
Bài 2 giúp mình ý c thôi ạ ^^
Bài 3 : Tìm x, biết: \(^{x^2+2015x-2014=2\sqrt{2017x-2016}}\)
Mình cần gấp, mong các bạn giúp.
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH= 3,6cm. CH= 6,4cm. a) Tính độ dài các đoạn thẳng AB, góc ACB (góc làm tròn đến độ.) b) Trên cạnh AC lấy điểm M (M khác A; M khác C), kẻ AK vuông góc với BM tại K. Chứng minh rằng: BK.BM=BH.BC, từ đó suy ra tam giác BHK đồng dạng với tam giác BMC.
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH= 3,6cm. CH= 6,4cm. a) Tính độ dài các đoạn thẳng AB, góc ACB (góc làm tròn đến độ.) b) Trên cạnh AC lấy điểm M (M khác A; M khác C), kẻ AK vuông góc với BM tại K. Chứng minh rằng: BK.BM=BH.BC, từ đó suy ra tam giác BHK đồng dạng với tam giác BMC.
Cho tam giác ABC vuông tại A, đường cao AH .Biết BH4cm,CH9cm.a)Tính độ dài các đoạn AH,AB,ACb)Tính số đo góc B và góc C của tam giác ABC( Làm tròn số đo góc đến phút)c)Qua B, kẻ đường thẳng (d) vuông góc với BC và cắt đường thẳng CA tại K. Chứng minh:BH.BCAK.ACd)Gọi I là trung điểm AB. Hạ ID vuông góc BC tại D. Tam giác ABC cần thêm điều kiện gì để AB^2 CD^2-BD^2Mình làm được 3 câu trên rồi .Các bạn giúp mình câu cuối với !!! Cảm ơn nhiều !!!
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH .Biết BH=4cm,CH=9cm.
a)Tính độ dài các đoạn AH,AB,AC
b)Tính số đo góc B và góc C của tam giác ABC( Làm tròn số đo góc đến phút)
c)Qua B, kẻ đường thẳng (d) vuông góc với BC và cắt đường thẳng CA tại K. Chứng minh:BH.BC=AK.AC
d)Gọi I là trung điểm AB. Hạ ID vuông góc BC tại D. Tam giác ABC cần thêm điều kiện gì để AB^2 =CD^2-BD^2
Mình làm được 3 câu trên rồi .Các bạn giúp mình câu cuối với !!! Cảm ơn nhiều !!!
Cho tam giác ABC vuông tại A, có AC AB và đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, ACa, Chứng minh AD.AB AE.AC và tam giác ABC đồng dạng với tam giác AEDb, Cho biết BH 2 cm, HC 4,5 cm:i, Tính độ dài đoạn thẳng DEii, Tính số đo góc ABC (làm tròn đến độ)iii, Tính diện tích tam giác ADE
Đọc tiếp
Cho tam giác ABC vuông tại A, có AC > AB và đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, AC
a, Chứng minh AD.AB = AE.AC và tam giác ABC đồng dạng với tam giác AED
b, Cho biết BH = 2 cm, HC = 4,5 cm:
i, Tính độ dài đoạn thẳng DE
ii, Tính số đo góc ABC (làm tròn đến độ)
iii, Tính diện tích tam giác ADE
Cho tam giác ABC có ba cạnh AB, AC, BC lần lượt là 2cm, 3cm, 4cm. Kẻ đường cao AH. Tính
a) Độ dài các đoạn thẳng BH, CH, AH.
b) Độ dài đường cao ứng với cạnh AB, AC
c) Số đo các góc A , B , C của tam giác ABC ( làm tròn đến phút )
Cho tam giác ABC vuông tại A có AH là đường cao. Biết BH 7,2cm và HC 12,8cm . a) Tính độ dài các đoạn AH , AC . b) Gọi I là trung điểm BC . Tính số đo góc ACB và góc IAC (làm tròn đến phút). c) Chứng minh: sin 2C = 2sinC.cosC
Cho tam giác ABC vuông tại A, biết AC = 20cm ; BC = 30cm.
a/ Giải tam giác vuông ABC ( Số đo của góc làm tròn đến độ )
b/ Kẻ đường cao AH của ΔABC. Tính AH ; CH.
c/ Chứng minh : tan2C = \(\dfrac{BH}{CH}\)