Question

: Cho tam giác ABC vuông tại B, phân giác AD. Từ D kẻ DH vuông góc với AC (H vuông gócAC); HD và AB kéo dài cắt nhau tại I. Chứng minh rằng: a) tam giác ABD= tam giác AHD . b) tam giác BDI = tam giácHDC . c) tam giácAIC cân. d) BC> AC+ AD- 2AB

Answer 1

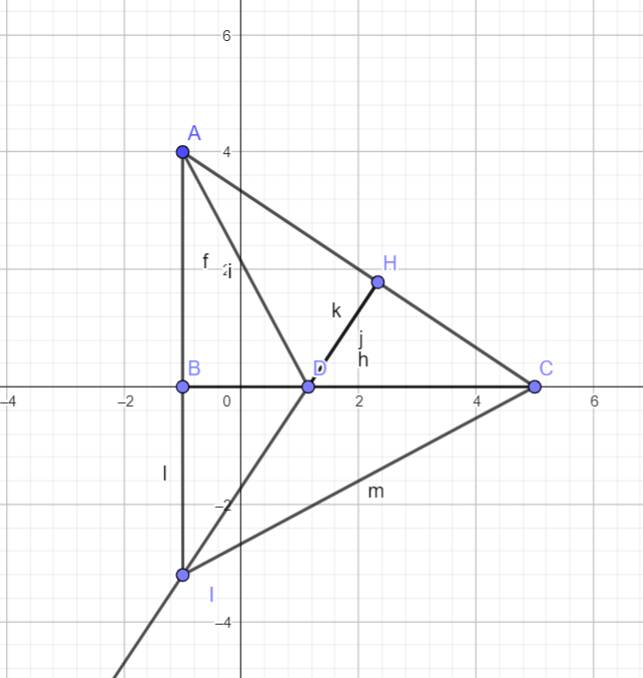
a: Xét ΔABD vuông tại B và ΔAHD vuông tại H có

AD chung

\(\widehat{BAD}=\widehat{HAD}\)

Do đó: ΔABD=ΔAHD

b: ΔABD=ΔAHD

=>DB=DH

Xét ΔDBI vuông tại B và ΔDHC vuông tại H có

DB=DH

\(\widehat{BDI}=\widehat{HDC}\)(hai góc đối đỉnh)

Do đó: ΔDBI=ΔDHC

c: ΔDBI=ΔDHC

=>BI=HC

ΔABD=ΔAHD

=>AB=AH

Ta có: AB+BI=AI

AH+HC=AC

mà AB=AH và BI=HC

nên AI=AC

=>ΔAIC cân tại A

Answer 2