Question

Cho tam giác ABC  vuông tại A.Kẻ phân giác trong AD của BAC ( với D ϵ BC ), biết DB =15cm, DC =20cm. Tính độ dài các đoạn thẳng AB ,AC
                                 ĐS: AB≈ 3,5cm , AC ≈ 4.7 cm

Answer 1

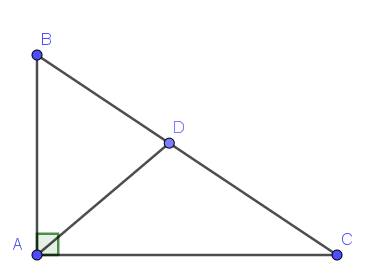
BC=BD+CD

=15+20

=35(cm)

Xét ΔABC có AD là phân giác

nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)

=>\(\dfrac{AB}{15}=\dfrac{AC}{20}\)

=>\(\dfrac{AB}{3}=\dfrac{AC}{4}=k\)

=>AB=3k; AC=4k

Ta có: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(\left(3k\right)^2+\left(4k\right)^2=35^2\)

=>\(25k^2=35^2\)

=>\(k^2=49\)

=>k=7

=>\(AB=3\cdot7=21\left(cm\right);AC=4\cdot7=28\left(cm\right)\)

Answer 2

Lời giải:

Theo tính chất đường phân giác: 

$\frac{AB}{AC}=\frac{BD}{DC}=\frac{15}{20}=\frac{3}{4}$

$\Rightarrow AB=\frac{3}{4}AC$
Theo định lý Pitago:

$AB^2+AC^2=BC^2=(BD+DC)^2=(15+20)^2=35^2$
$\Rightarrow (\frac{3}{4}AC)^2+AC^2=35^2$
$\Rightarrow AC^2.\frac{25}{16}=35^2$
$\Rightarrow AC^2=784\Rightarrow AC=28$ (cm)

$AB=\frac{3}{4}AC=\frac{3}{4}.28=21$ (cm)

Answer 3

Đáp số bạn đưa ra chưa đúng.

Answer 4

Hình vẽ: