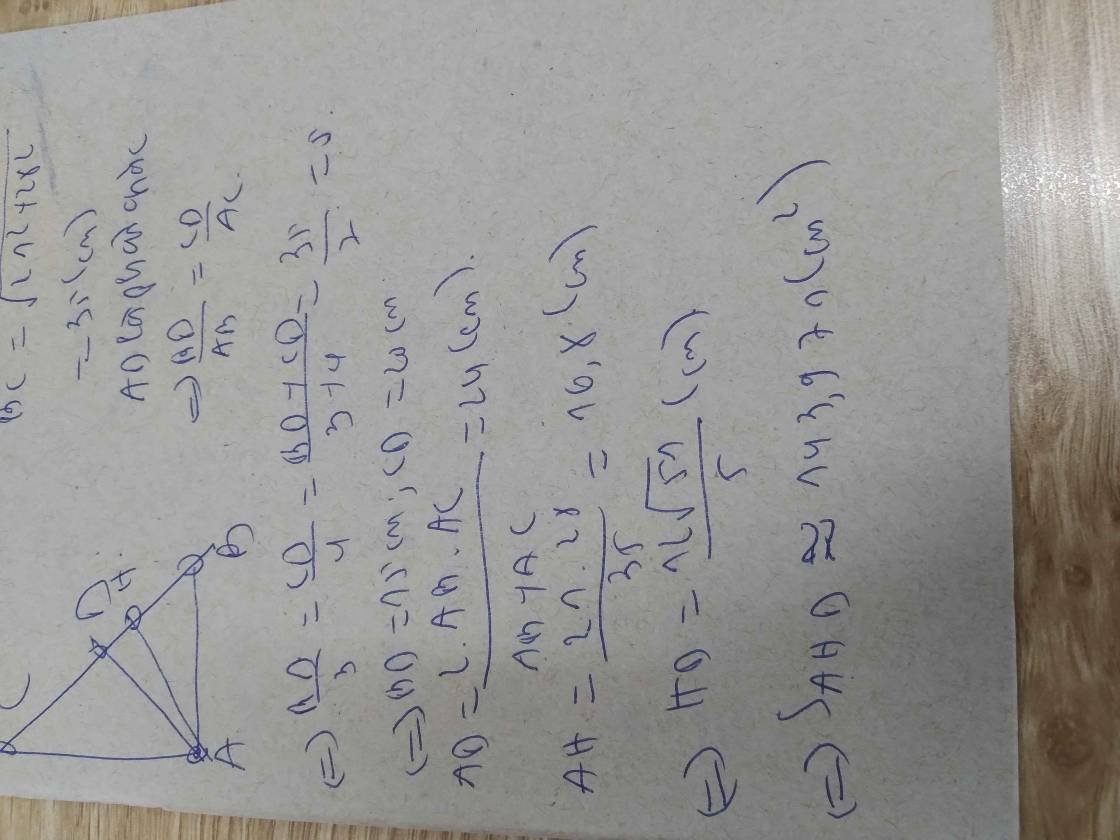Question

Cho tam giác ABC vuông tại A(góc A=90°),AB=21cm,AC=28cm. Vẽ đường cao AH(H thuộc BC). Tia phân giác của góc A cắt BC tại D. Tính BC,BD,CD và diện tích tam giác AHD

Answer 1

Xét ΔABC vuông tại A, áp dụng định lí py-ta-go ta có:

\(BC^2=AB^2+AC^2\)

         \(=21^2+28^2\)

         \(=1225\)

->\(BC=\sqrt{1225}=35\left(cm\right)\)

Xét ΔABC có AD là tia phân giác ta có:

\(\dfrac{AB}{BD}=\dfrac{AC}{CD}=\dfrac{AB+AC}{BC}hay\dfrac{21}{BD}=\dfrac{28}{CD}=\dfrac{21+28}{35}=\dfrac{7}{5}\)

⇒\(BD=\dfrac{21.5}{7}=15\left(cm\right)\)

⇒\(CD=\dfrac{28.5}{7}=20\left(cm\right)\)

 

Answer 2