a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay \(BC=\sqrt{193}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{\sqrt{193}}\)
\(\Leftrightarrow\widehat{B}\simeq60^0\)
\(\Leftrightarrow\widehat{C}=30^0\)
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay \(BC=\sqrt{193}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{\sqrt{193}}\)
\(\Leftrightarrow\widehat{B}\simeq60^0\)
\(\Leftrightarrow\widehat{C}=30^0\)
Cho tam giác ABC vuông tại A, AB= 12cm, BC= 20cm. Giải tam giác ABC
Cho tam giác ABC vuông tại A. Gọi BC = a, AC = b, AB = c. Giải tam giác ABC, biết:
a, b = 10 cm, C ^ = 30 0
b, a = 20cm,
B
^
=
35
0
c, a = 15cm, b = 10cm
d, b = 12cm, c = 7cm
Cho tam giác ABC vuông tại A có: BC = 20cm; AC = 12cm. Quay tam giác ABC cạnh AB ta được một hình nón có thể tích là:
A. 2304 π ( c m 3 )
B. 1024 π ( c m 3 )
C. 786 π ( c m 3 )
D. 768 π ( c m 3 )
Cho tam giác ABC vuông tại A có: BC = 20cm; AC = 12cm. Quay tam giác ABC cạnh AB ta được một hình nón có thể tích là:
A. 2304 π ( c m 3 )
B. 1024 π ( c m 3 )
C. 786 π ( c m 3 )
D. 768 π ( c m 3 )
Cho tam giác ABC có AB=12cm, AC=16cm, BC=20cm.
a, Chứng minh: tam giác ABC vuông tại A
b, Tính đường cao AH
c, Chứng minh: AB.cosB + AC.cosC = 20cm
Cho tam giác ABC vuông tại A, AB = 15cm; AC = 20cm. Phân giác của góc A cắt BC tại E.
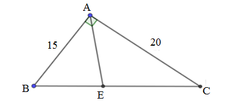
Giải tam giác ABC:
A. BC = 25; B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
B. BC = 25; B ^ = 53 0 8 ' ; C ^ = 53 0 8 '
C. BC = 25; B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
D. BC = 25; B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
Cho tam giác ABC vuông tại A có AC= 12cm, BC=15cm. Giải tam giác ABC?