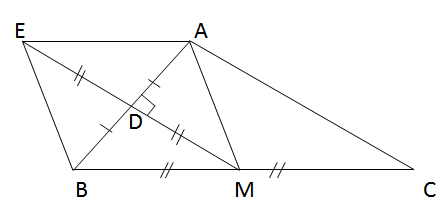
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D
a) Chứng minh rằng điểm E đối xứng với M qua AB
b) Các tứ giác AEMC, AEBM là hình gì ? Vì sao ?
c) Cho BC = 4cm, tính chu vi tứ giác AEBM
d) Tam giác vuông ABC có điều kiện gì thì AEBM là hình vuông ?
a) Ta có: E và M đối xứng với nhau qua D
=> DE = DM ; ME vuông góc AB
Ta có BD = DA ( D là trung điểm AB )
mà ME vuông góc AB ( cmt )
=> AB là trung trực của ME hay E và M đối xứng nhau qua D
b) Xét Tam giác ABC có:
M là trung điểm BC ( gt )
D là trung điểm AB ( gt)
=> DM là đường trung bình tam giác ABC
=> DM // AC;
mà E thuộc DM
nên EM // AC
Xét tứ giác AEMC có:
EM // AC ( cmt)
EM = AC ( cùng = 2DM )
=> Tứ giác AEMC là hình bình hành
Xét tứ giác AEBM có:
ED = DM ( gt )
DB = AD ( gt )
=> Tứ giác AEBM là hình bình hành
mà AB vuông góc EM
=> AEBM là hình thoi
c, Ta có : AM = ( trung tuyến ứng với cạnh huyền)
=> AM = (cm)
Chu vi hình thoi AEBM:
2 . 4 =8 (cm)
d, Nếu AEBM là hình vuông
thì = góc B= góc M= 90 độ
<=> AM vuông góc BC
<=> AM vừa là đường trung tuyến vừa là đường cao tam giác ABC
<=> Tam giác ABC vuông cân tại A
Vậy tam giác ABC vuông cân ở A thì AEBM là hình vuông
a) Ta có: MB = MC (giả thiết) ; DA = DB (Giả thiết)
⇒ DM là đường trung bình của Δ ABC
⇒ DM//AC
Mặt khác ABC vuông tại A
⇒ AC ⊥ AB ⇒ DM ⊥ AB
⇒ DE ⊥ AB (*)
E là điểm đối xứng với M qua D
⇒ DM = DE (**)
Từ (*) và (**) ta suy ra: Điểm E đối xứng với M qua AB
b) Ta có AB ⊥ EM và DE = DM, DA = DB
⇒ Tứ giác AEBM là hình thoi
⇒ AE//BM mà BM = MC ⇒ AE//MC và AE = MC
⇒ tứ giác AEMC là hình bình hàng
c) Ta có BC = 4 (cm) ⇒ BM = BC/2 = 2(cm)
Chu vi hình thoi ABEM là : P = 4BM = 8 (cm)
d) Hình thoi AEBM là hình vuông khi góc ∠AMB = 90 \(^0\)
⇒ AM ⊥ BC
Mặt khác: AM là trung tuyến của tam giác vuông ABC
Suy ra: Δ ABC vuông cân tại A
Điều kiện: Δ ABC vuông cân tại A
a) Ta có: MB = MC (giả thiết)
DA = DB (Giả thiết)
⇒ DM là đường trung bình của Δ ABC
⇒ DM//AC
Mặt khác ABC vuông tại A
⇒ AC ⊥ AB ⇒ DM ⊥ AB ⇒ DE ⊥ AB (*)
E là điểm đối xứng với M qua D ⇒ DM = DE (**)
Từ (*) và (**) ta suy ra: Điểm E đối xứng với M qua AB
b) Ta có AB ⊥ EM và DE = DM, DA = DB
⇒ Tứ giác AEBM là hình thoi
⇒ AE//BM mà BM = MC ⇒ AE//MC và AE = MC
⇒ tứ giác AEMC là hình bình hàng
c) Ta có BC = 4 (cm) ⇒ BM = BC/2 = 2(cm)
Chu vi hình thoi ABEM là P = 4BM = 8 (cm)
d) Hình thoi AEBM là hình vuông khi góc ∠AMB = 900
⇒ AM ⊥ BC
Mặt khác: AM là trung tuyến của tam giác vuông ABC
Suy ra: Δ ABC vuông cân tại A
Điều kiện: Δ ABC vuông cân tại A
a) Xét \(\Delta ABC\) có : \(DA = DB (gt)\)
\(MB=MC\)\((gt)\)
\(\Rightarrow DM\) là đường trung bình của \(\Delta ABC\)
\(\Rightarrow DM\)\(\parallel AC\) và \(DM=\dfrac{1}{2}AC\)
\(\Rightarrow\widehat{A}+\widehat{D_1}=180^0\),mà \(\widehat{A}=90^0\)
\(\Rightarrow\widehat{D_1=90^0,\Rightarrow AB\perp EM}\) tại \(D\)
mà \(DE = DM\)
\(\Rightarrow AB\) là đường trung trực của \(EM\)
Hay : \(E\) đối xứng \(M\) qua \(AB\)
b) Ta có : \(DM \parallel AC(cmt)\)
\(\Rightarrow\) \(EM\parallel AC\) \((1)\)
\(DM=\dfrac{1}{2}AC\left(cmt\right),DM=ED\)
\(\Rightarrow EM=AC\) \((2)\)
Từ \((1)\) và \((2)\),suy ra : Tứ giác \(AEMC \) là hình bình hành
Xét tứ giác \(AEBM \) có :
\(ED=DM\left(gt\right)\)
\(DB=DA(gt)\)
\(\Rightarrow\) Tứ giác \(AEBM\) là hình bình hành
Lại có : \(ME\perp AB\)
\(\Rightarrow\) Tứ giác \(AEBM\) là hình thoi
c) Ta có : \(BM=\dfrac{1}{2}BC=\dfrac{1}{2}.4=2\left(cm\right)\)
Chu vi tứ giác \(AEBM\) là :
\(BM.4=2.4=8(cm)\)
d) Để hình thoi \(AEBM\) trở thành hình vuông,thì :
\(AE=EM\)\(,\)mà \(EA=AC\)
\(\Rightarrow AB=AC\)
Vậy để hình thang \(AEBM\) trở thành hình vuông,thì :
\(\Delta ABC\) vuông cân tại \(A\)





