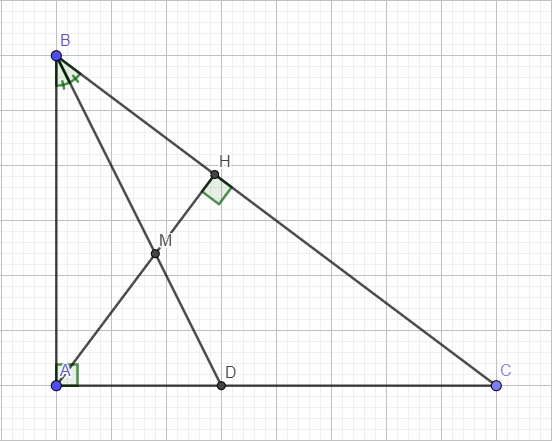
a.
Xét hai tam giác BAC và BHA có:
\(\left\{{}\begin{matrix}\widehat{ABH}\text{ chung}\\\widehat{BAC}=\widehat{BHA}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta BAC\sim\Delta BHA\left(g.g\right)\)
b.
Áp dụng định lý Pitago cho tam giác vuông ABC:
\(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\)
Do \(\Delta BAC\sim\Delta BHA\Rightarrow\dfrac{BC}{AB}=\dfrac{AC}{AH}\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3.4}{5}=\dfrac{12}{5}\)
Áp dụng định lý Pitago cho tam giác vuông ABH:
\(BH=\sqrt{AB^2-AH^2}=\dfrac{9}{5}\)
\(CH=BC-BH=\dfrac{16}{5}\)
c.
Do BD là phân giác góc B, áp dụng định lý phân giác cho tam giác ABC:
\(\dfrac{DC}{AD}=\dfrac{BC}{AB}\) (1)
Áp dụng định lý phân giác cho tam giác ABH:
\(\dfrac{AM}{HM}=\dfrac{AB}{BH}\) (2)
Lại có \(\Delta BAC\sim\Delta BHA\Rightarrow\dfrac{BC}{AB}=\dfrac{AB}{BH}\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{DC}{AD}=\dfrac{AM}{HM}\Rightarrow AM.AD=HM.CD\)