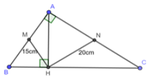
Xét ∆ ABC vuông tại A có M là trung điểm AB
=> HM là đường trung tuyến ứng với cạnh huyền AB
=> HM = 1 2 AB => AB = 2HM = 2. 15 = 30 (cm)
Xét ∆ ACH vuông tại H có N là trung điểm AC
=> HN là đường trung tuyến ứng với cạnh huyền AC
=> HN = 1 2 AC => AC = 2HN = 2. 20 = 40 (cm)
Áp dụng định lý Pitago cho ABH vuông tại A có:
![]()
![]()
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
![]()
Ta có: HC = BC – BH = 50 – 18 = 32 (cm)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
AH.BC = AB.AC => AH.50 = 30.40 => AH = 24 (cm)
Đáp án cần chọn là: D

