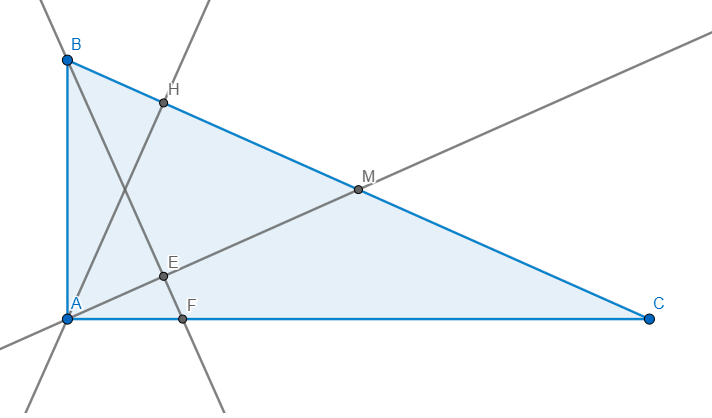
a) tam giác ABC vuông tại A có AM là trung tuyến \(\Rightarrow AM=\dfrac{BC}{2}\)
Ta có: \(2BH.AM=BH.2AM=BH.BC=AB^2\)
b) tam giác BAF vuông tại A có đường cao AE
\(\Rightarrow BE.BF=BA^2=BH.BC\)
Ta có: \(AM=\dfrac{BC}{2}=BM\Rightarrow\Delta ABM\) cân tại M
\(\Rightarrow\angle MAB=\angle MBA\) mà \(\angle MAB=\angle BFA\Rightarrow\angle ABC=\angle BFA\)
Xét \(\Delta ABF\) và \(\Delta ACB:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\angle ABC=\angle BFA\end{matrix}\right.\)
\(\Rightarrow\Delta ABF\sim\Delta ACB\left(g-g\right)\Rightarrow\dfrac{AB}{AC}=\dfrac{AF}{AB}\Rightarrow AB^2=AF.AC\)
\(\Rightarrow BE.BF=BH.BC=AF.AC\)