Trong tam giác ABC vuông tại A nên ta có:
A B 2 = BH.BC =2.(2+6)=2.8=16
suy ra AB = 4cm
Diện tích hình tròn tâm (O) là :
S=π. A B / 2 2 = π. 4 / 2 2 = 4π ( c m 2 )
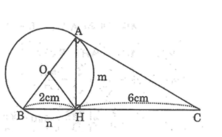
Cho tam giác ABC vuông ở A và đường cao AH.Vẽ đường tròn tam O đường kính AB.Biết BH = 2cm và HC = 6cm.Tính: Diện tích hình quạt tròn AOH (ứng với các cung nhỏ AH)
Cho tam giác ABC vuông ở A và đường cao AH.Vẽ đường tròn tam O đường kính AB.Biết BH = 2cm và HC = 6cm.Tính: Tổng diện tích hai hình viên phân AmH và BnH (ứng với các cung nhỏ)
Giải hộ mình với mai thi rồi
Cho tam giác ABC vuông tại A và đường cao AH vẽ đường tròn O đường kính AB, Biết BH = 2cm ; CH = 6cm. Tính :
a. Diện tích hình tròn
b. Diện tích hình quạt tròn AOH ( Ứng với cung tròn AH )
Cho tam giác ABC vuông tại A , đường cao AH.Vẽ đường tròn tâm O đường kính AH. Đường tròn này cắt các cạnh AB, Ác theo thứ tự ở D và E.
a) CMR: D, O , E thẳng hàng .
B) các tiếp tuyến của đường tròn tâm Ở kẻ từ D và E cắt BC lần lượt tại M,N.CMR: M và N là trung điểm của HB và HC
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (O) đường kính BH và đường tròn tâm O' đường kính CH, hai đường tròn này cắt AB, AC thứ tự tại E và F
a, Tứ giác AEHF là hình gì?
b, Chứng minh EF là tiếp tuyến chung của (O) và (O’)
c, Chứng minh đường tròn đường kính OO' tiếp xúc với EF
d, Cho đường tròn tâm I bán kính r tiếp xúc với EF, (O) và (O’). Tính r theo BH và CH?
Cho tam giác ABC nội tiếp đường tròn tâm O,đường kính BC , đường cao AH
1> Cho BH = 9,HC=16.Tính AH,AB,AC và bán kính đường tròn nội tiếp tam giác ABC
2>Vẽ đường tròn tâm I,đường kính AH. Đường tròn tâm I cắt AB ở D,cắt AC ở E và cắt đường tròn tâm O ở K ,K khác A.
Chứng minh AEHD là Hình Chữ Nhật và D,I,E thẳng hàng
3> Chứng minh 0A vuông góc với DE
4>AK cắt BC ở F.Chứng minh F,D,E thẳng hàng
Cho tam giác ABC vuông tại A, đường cao AH. Dựng đường tròn tâm O đường kính AB. Cho biết số đo góc ABC = 60 độ và AB = a . Tính theo a diện tích phần tam giác. ABC nằm ngoài đường tròn (O)
cho tam giác abc vuông tại a, đường cao ah.vẽ đường tròn tâm o đường kính ah. đường tròn cắt ab ,ac tại m,n. Chứng minh bmnc cùng thuộc một đường tròn ?
