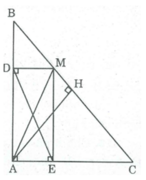
Gọi H là trung điểm của BC
Suy ra: AH ⊥ BC (tính chất tam giác cân)
Do đó, AM ≥ AH ( quan hệ đường vuông góc và đường xiên )(dấu " = " xảy ra khi M trùng với H)
Tứ giác ADME là hình chữ nhật .
⇒ AM = DE (tính chất hình chữ nhật)
Suy ra: DE ≥ AH
Vậy DE có độ dài nhỏ nhất là AH khi và chỉ khi điểm M là trung điểm của BC.

