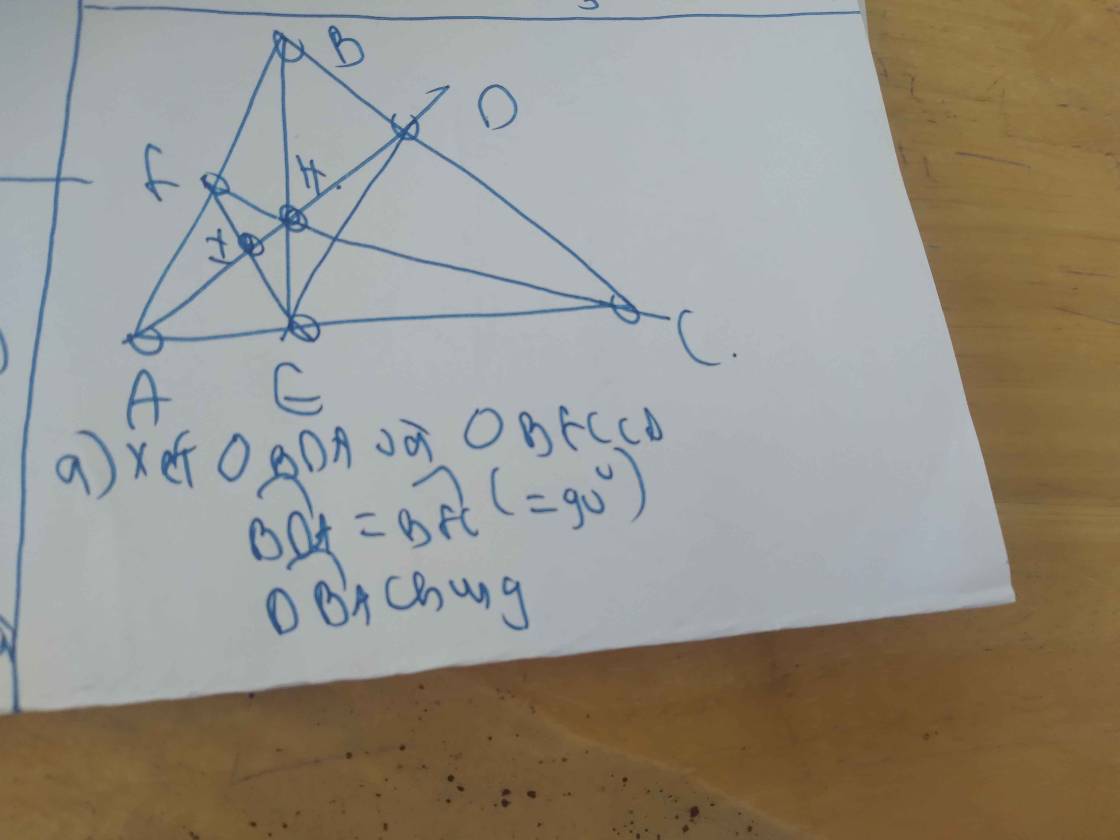
Cho tam giác ABC nhọn, có các đường cao AD;BE;CF cắt nhau tại H.
a) Chứng minh tam giác BAD đồng dạng với tam giác BFC, từ đó => BD x BC = BF x BA
b) Chứng minh góc BDF = góc BAC
c) Chứng minh EB là tia phân giác góc FED
d) AD cắt EF tại I. Chứng minh HI x AD = HD x AI
e) BH x BE = BD x BC
f) Chứng minh HB x BE + HC x CF = \(BC^2\)
g) Đường thẳng đi qua A song song với BC cắt DF tại M. CM cắt AB tại K. Chứng minh KE song song với BC