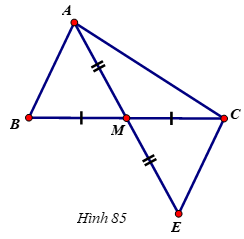
a: Xét ΔAMB và ΔEMC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔAMB=ΔEMC
b: Ta có: ΔAMB=ΔEMC
=>AB=CE
Ta có: ΔAMB=ΔEMC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//EC
c: Xét ΔHAM và ΔKEM có
HA=KE
\(\widehat{HAM}=\widehat{KEM}\)
AM=EM
Do đó: ΔHAM=ΔKEM
=>\(\widehat{AMH}=\widehat{EMK}\)
mà \(\widehat{AMH}+\widehat{HME}=180^0\)(hai góc kề bù)
nên \(\widehat{EMK}+\widehat{HME}=180^0\)
=>H,M,E thẳng hàng
Đúng 1
Bình luận (0)