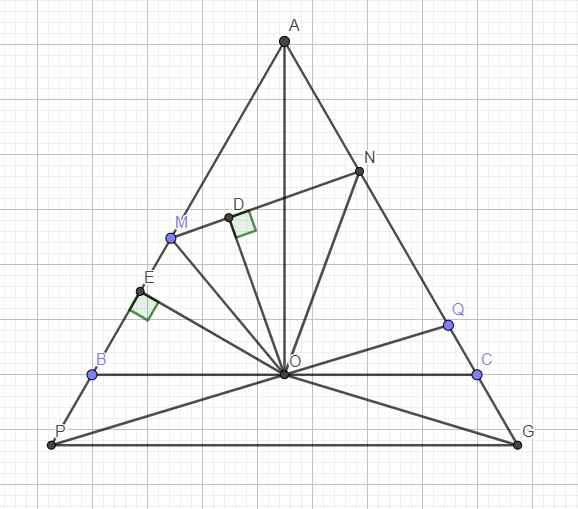
Cho tam giác ABC đều có cạnh bằng a. Gọi O là trung điểm của BC. Một góc xOy bằng 60o quay quanh điểm O sao cho hai cạnh Ox, Oy luôn cắt AB và AC lần lượt tại M và N.
a) cm: Tam giác OBM đồng dạng với tam giác NCO.
b) cm: BC2=4BM.CN.
c) Khoảng cách từ điểm O đến MN không đổi khi Ox; Oy thay đổi.
d) Từ O vẽ đường thẳng d bất kì cắt AB; AC tại P; Q.
CMR: \(\dfrac{1}{AP}+\dfrac{1}{AQ}\) không đổi.
a.
a.
\(\widehat{BMO}+\widehat{B}+\widehat{BOM}=\widehat{BOM}+\widehat{MON}+\widehat{CON}=180^0\)
\(\Rightarrow\widehat{BMO}=\widehat{CON}\) (do \(\widehat{B}=\widehat{MON}=60^0\))
\(\Rightarrow\left\{{}\begin{matrix}\widehat{B}=\widehat{C}=60^0\\\widehat{BMO}=\widehat{CON}\end{matrix}\right.\) \(\Rightarrow\Delta OBM\sim\Delta NCO\) (g.g)
b.
Từ câu a \(\Rightarrow\dfrac{OB}{CN}=\dfrac{BM}{OC}\Rightarrow OB.OC=BM.CN\Rightarrow\dfrac{BC}{2}.\dfrac{BC}{2}=BM.CN\Rightarrow...\)
c.
Lần lượt kẻ OD và OE vuông góc MN và AB.
Do O cố định \(\Rightarrow\) OE cố định
Từ câu a ta có: \(\dfrac{BM}{OC}=\dfrac{OM}{ON}\Rightarrow\dfrac{BM}{OM}=\dfrac{OC}{ON}=\dfrac{OB}{ON}\) (1)
Đồng thời \(\widehat{B}=\widehat{MON}=60^0\) (2)
(1);(2) \(\Rightarrow\Delta OBM\sim\Delta NOM\left(c.g.c\right)\Rightarrow\widehat{BMO}=\widehat{OMN}\)
\(\Rightarrow\Delta_VOME=\Delta_VOMD\left(ch-gn\right)\)
\(\Rightarrow OD=OE\), mà OE cố định \(\Rightarrow OD\) cố định
d.
Không mất tính tổng quát, giả sử d cắt AB, AC như hình vẽ bên dưới
Trên tia AC lấy G sao cho \(AG=AP\Rightarrow\Delta APG\) đều (tam giác cân 1 góc 60 độ)
\(\Rightarrow\) AO đồng thời là trung trực PG
\(\Rightarrow OP=OG\Rightarrow\Delta OBP=\Delta OCG\left(c.c.c\right)\)
\(\Rightarrow\widehat{QOC}=\widehat{BOP}\left(đối-đỉnh\right)=\widehat{COG}\Rightarrow OC\) là phân giác \(\widehat{QOG}\) và OA là phân giác ngoài đỉnh O tam giác OQG
\(\Rightarrow\dfrac{CQ}{CG}=\dfrac{OQ}{OG}=\dfrac{AQ}{AG}\) theo định lý phân giác \(\Rightarrow\dfrac{CQ}{AQ}=\dfrac{CG}{AG}\)
\(\Rightarrow\dfrac{AC-AQ}{AQ}=\dfrac{AG-AC}{AG}\Rightarrow\dfrac{AC}{AQ}-1=1-\dfrac{AC}{AG}\)
\(\Rightarrow AC\left(\dfrac{1}{AQ}+\dfrac{1}{AG}\right)=2\Rightarrow\dfrac{1}{AQ}+\dfrac{1}{AG}=\dfrac{2}{AC}\)
\(\Rightarrow\dfrac{1}{AQ}+\dfrac{1}{AP}=\dfrac{2}{AC}\) không đổi