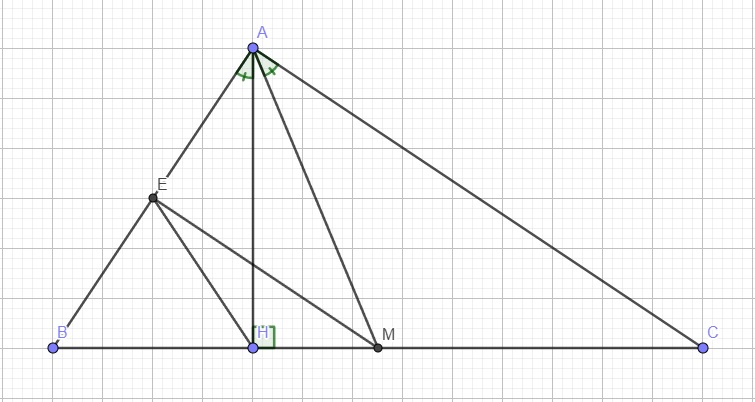
a.
Do E là trung điểm AB, M là trung điểm BC
\(\Rightarrow\) EM là đường trung bình tam giác ABC
\(\Rightarrow EM||AC\)
\(\Rightarrow\widehat{MAC}=\widehat{AME}\) (so le trong) (1)
Trong tam giác vuông AHB, HE là trung tuyến ứng với cạnh huyền
\(\Rightarrow HE=\dfrac{1}{2}AB=AE\) \(\Rightarrow\Delta AHE\) cân tại E
\(\Rightarrow\widehat{AHE}=\widehat{BAH}\) (2)
Mà \(\widehat{BAH}=\widehat{MAC}\) (giả thiết) (3)
(1);(2);(3) \(\Rightarrow\widehat{AME}=\widehat{AHE}\)
\(\Rightarrow AMHE\) nội tiếp (2 góc bằng nhau cùng chắn AE)
\(\Rightarrow\) 4 điểm A, E, M, H cùng thuộc 1 đường tròn
b.
Theo cmt AMHE nội tiếp \(\Rightarrow\widehat{AEM}=\widehat{AHM}=90^0\) (cùng chắn AM)
\(\Rightarrow EM\perp AB\)
Mà \(EM||AC\)
\(\Rightarrow AB\perp AC\)
\(\Rightarrow\widehat{BAC}=90^0\)