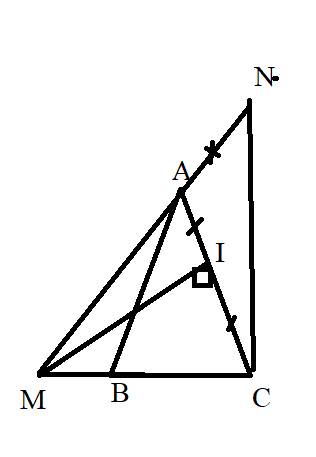
a: Xét ΔMAC có
MI là đường cao
MI là đường trung tuyến
Do đó: ΔMAC cân tại M
=>\(\widehat{AMC}=180^0-2\cdot\widehat{ACM}=180^0-2\cdot\widehat{ACB}\left(1\right)\)
ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ACB}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{AMC}=\widehat{BAC}\)
b:
ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\)
\(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{ABM}=180^0-\widehat{ABC}=180^0-\widehat{ACB}\left(3\right)\)
\(\widehat{CAN}+\widehat{CAM}=180^0\)(hai góc kề bù)
=>\(\widehat{CAN}+\widehat{ACB}=180^0\)
=>\(\widehat{CAN}=180^0-\widehat{ACB}\left(4\right)\)
Từ (3) và (4) suy ra \(\widehat{ABM}=\widehat{CAN}\)
Xét ΔABM và ΔCAN có
AB=CA
\(\widehat{ABM}=\widehat{CAN}\)
BM=AN
Do đó;ΔABM=ΔCAN
c: ΔABM=ΔCAN
=>NC=MA
mà MA=MC
nên NC=MC
\(\widehat{AMC}=\widehat{BAC}\)
mà \(\widehat{BAC}=45^0\)
nên \(\widehat{AMC}=45^0\)
Xét ΔCMN có CM=CN và \(\widehat{CMN}=45^0\)
nên ΔCMN vuông cân tại C