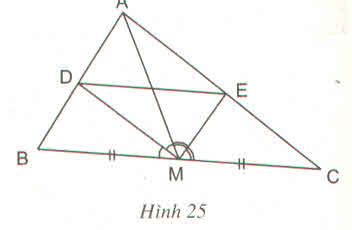
Vì AM là đường trung trực kẻ từ A nên=>\(\Delta\)ABC cân ở A:
Ta có :
\(\widehat{BMD}=\widehat{BMA}=90^0:2=45^0\)
\(\widehat{CME}=\widehat{EMA}=90^0:2=45^0\)
=>\(\widehat{BMD}=\widehat{DMA}=\widehat{AME}=\widehat{EMC}\)
Xét \(\Delta\)DBM và \(\Delta\)ECM có:
BM=MC(do AM là đường trung trực)
\(\widehat{ABC}=\widehat{ACB}\)( do \(\Delta\)ABC cân ở A)
\(\widehat{BMD}=\widehat{CME}(cmt)\)
=>\(\Delta\)DMB=\(\Delta\)EMC(g-c-g)
=>BD=EC(hai cạnh tương ứng)
Lại có : BD+AD=AB; AE+EC=AC
MÀ AB=AC=> BD+AD=AE+EC
Mà BD=EC=> AD=AE
Xét AD=AE;BD=EC
=> \(\dfrac{AD}{BD}=\dfrac{AE}{EC}\)
=> DE//BC( Định lý Ta - lét đảo)