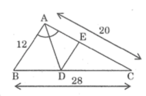
Xét ΔBAC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{12}=\dfrac{CD}{20}\)
mà BD+CD=28cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{12}=\dfrac{CD}{20}=\dfrac{BD+CD}{12+20}=\dfrac{28}{32}=\dfrac{7}{8}\)
Do đó: BD=10,5cm; CD=17,5cm
Xét ΔBAC có
DE//AB
nên \(\dfrac{DE}{AB}=\dfrac{CD}{BC}\)
\(\Leftrightarrow DE=\dfrac{17.5}{28}\cdot12=7.5\left(cm\right)\)