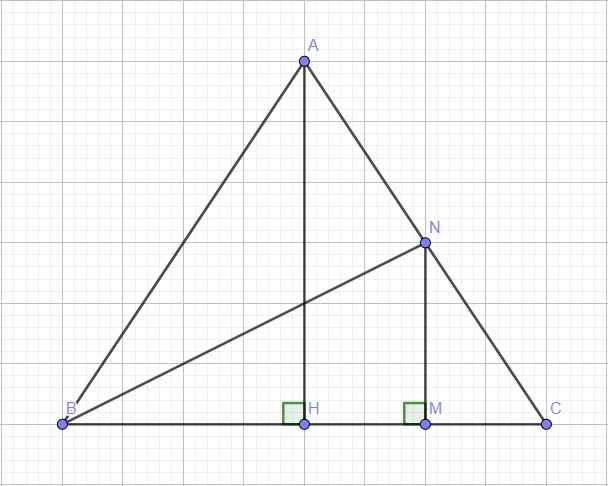
Do AH là đường cao trong tam giác ABC cân tại A nên AH cùng là đường trung tuyến
\(\Rightarrow\)H là trung điểm của BC
Áp dụng định lý py-ta-go vào tam giác vuông AHC có:
\(HC=\sqrt{AC^2-AH^2}=\sqrt{2}\left(cm\right)\)
Do M là trung điểm của HC\(\Rightarrow HM=\dfrac{HC}{2}=\dfrac{\sqrt{2}}{2}\) (cm)
Áp dụng định lý py-ta-go vào tam giác AMH vuông có:
\(AH^2+HM^2=AM^2\)
\(\Leftrightarrow AM=\sqrt{AH^2+HM^2}=\sqrt{3+\dfrac{1}{2}}=\dfrac{\sqrt{14}}{2}\left(cm\right)\)
Có M và H lần lượt là tđ của HC và CA
Suy ra MN là đường trung bình của tam giác AHC
\(\Rightarrow\) MN//AH và \(MN=\dfrac{AH}{2}=\dfrac{\sqrt{3}}{2}\)(cm)
Vì \(AH\perp BC\)\(\Rightarrow MN\perp BC\)
Áp dụng định lý py-ta-go vào tam giác BNM vuông có:
\(BN^2=MN^2+BM^2=\dfrac{3}{4}+\left(BC-MC\right)^2=\dfrac{3}{4}+\left(2HC-HM\right)^2=\dfrac{3}{4}+\dfrac{9}{2}=\dfrac{21}{4}\)
\(\Rightarrow BN=\dfrac{\sqrt{21}}{2}\) (cm)
Vậy...
Bạn nào giúp em với em sắp nộp bài rùi ạ!
\(AB=AC\Rightarrow\Delta ABC\) cân tại A \(\Rightarrow\) AH là đường cao đồng thời là trung tuyến hay H là trung điểm BC
\(\Rightarrow BH=CH\)
Pitago cho tam giác ACH: \(CH=\sqrt{AC^2-AH^2}=\sqrt{2}\)
\(\Rightarrow HM=\dfrac{1}{2}CH=\dfrac{\sqrt{2}}{2}\) \(\Rightarrow BM=BH+HM=CH+HM=\dfrac{3\sqrt{2}}{2}\)
Pitago tam giác AHM: \(AM=\sqrt{AH^2+HM^2}=\dfrac{\sqrt{14}}{2}\)
Do N là trung điểm AC, M là trung điểm HC \(\Rightarrow MN\) là đường trung bình tam giác ACH
\(\Rightarrow\left\{{}\begin{matrix}MN||AH\Rightarrow MN\perp BC\\MN=\dfrac{1}{2}AH=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
Pitago tam giác BMN: \(BN=\sqrt{BM^2+MN^2}=\dfrac{\sqrt{21}}{2}\)
áp dụng pytago \(=>HC=\sqrt{AC^2-AH^2}=\sqrt{5-3}=\sqrt{2}cm\)
M là trung điểm HC\(=>HM=MC=\dfrac{1}{2}HC=\dfrac{\sqrt{2}}{2}cm\)
theo pytago\(=>AM=\sqrt{HM^2+AH^2}=\sqrt{\left(\dfrac{\sqrt{2}}{2}\right)^2+3}=\dfrac{\sqrt{14}}{2}cm\)
có M,N là trung điểm HC,AC=>MN là đường trung bình tam giác AHC
\(=>MN//AH\) mà \(AH\perp BC=>MN\perp BC\)
cũng từ MN là đường trung bình \(=>MN=\dfrac{1}{2}AH=\dfrac{\sqrt{3}}{2}cm\)
do AB=AC=>tam giác ABC cân tại A có AH là đ cao đồng thời là trung tuyến
\(=>BH=HC=\sqrt{2}cm\)
áp dụng pytago\(=>BN=\sqrt{MN^2+\left(BH+HM\right)^2}\)
\(=\sqrt{\left(\dfrac{\sqrt{3}}{2}\right)^2+\left(\sqrt{2}+\dfrac{\sqrt{2}}{2}\right)^2}=\dfrac{\sqrt{21}}{2}cm\)