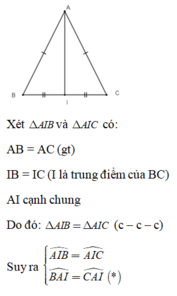
Lại có: I nằm giữa B và C (I là trung điểm BC) => Tia AI nằm giữa tia AB và tia AC (**)
Từ (*) và (**) suy ra AI là tia phân giác của B A C ^
Vậy cả A, B, C đều đúng.
Chọn đáp án D

Lại có: I nằm giữa B và C (I là trung điểm BC) => Tia AI nằm giữa tia AB và tia AC (**)
Từ (*) và (**) suy ra AI là tia phân giác của B A C ^
Vậy cả A, B, C đều đúng.
Chọn đáp án D
cho tam giác abc, i là điểm nằm trong tam giác và i cách đều hai cạnh ab và ac phát biểu nào là đúng
a/ ai, bi là các tia phân giác của góc a, b
b/ i là giao điểm của ba đường phân giác
c/ai là trung tuyến của bc
d/cả ba đề sai
Cho tam giác ABC ( AB< AC ). Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB = ID. Chứng minh : a) Δ AIB = Δ CID. b) AD = BC và AD // BC. c) Gọi E là trung điểm của AB. Trên tia đối của tia EC lấy điểm K sao cho: EC = EK. Chứng minh: D, A, K thẳng hàng.
Cho Δ ABC vuông tại B, BC = 15 cm, BA = 8 cm. Trên cạnh BC lấy E sao cho BE = BA
a) Tính AC
b) Δ ABE là tam giác gì? Vì sao
c) Từ B kẻ đường thẳng vuông với AE tại H và cắt AC tại D. Chứng minh BD là tia phân giác của góc ABC
d) Gọi I là giao điểm của đường thẳng AD và DE. Chứng minh A song song IC
Cho Δ ABC cân có góc A = 120°. Vẽ tia phân giác AI ( I ∈ BC ). Từ I vẽ IH vuông góc AB tại H, IK vuông góc AC tại K, trên đoạn HB lấy N sao cho HM = KN
a) Chứng minh Δ IMN cân
b) Chứng minh HK song song MN
c) Từ C vẽ đường thẳng d ⊥ BC cắt tia BA tại E. Biết CE = 8 cm. Tính CK và HK
THANKS MN
Cho ABC cân ở A. Có góc A nhọn Gọi I là trung điểm của BC . Kẻ BD vuông góc với AC tại D , kẻ CE vuông góc với AB tại E . Gọi K là giao điểm của BD và CE .
Chứng minh rằng: a) Δ BCE= ΔCBD
b) Δ BEK= ΔCDK và AK là tia phân giác của góc BAC
c) Ba điểm A,K,I thẳng hàng
1 ) Cho Δ ADE cân tại A . Trên cạnh DE lấy các điểm B và C sao cho DB = EC , nhỏ hơn 1/2 DE .
a ) Δ ABC là tam giác gì ?
b ) Vẽ BM ⊥ AD , CN ⊥ AE . Chứng minh : CM = CN
c ) Gọi I là giao điểm của MB và NC . Δ IBC là tam giác gì ?
d ) Chứng minh : AI là tia phân giác của góc BAC
2 ) Cho Δ ABC cân tại A . Vẽ BH ⊥ AC . Gọi D là 1 điểm thuộc cạnh đáy BC . Vẽ DE ⊥ AC , DF ⊥ AB . Chứng minh : DE + DF = BH
cho tam giác ABC, AB=AC, I là trung trực của điểm BC
a,CM Tam giác ABI=tamgiác ACI
b,CM AI là tia phân giác của góc BAC
c,CM AI vuông góc với BC
d,Gọi Cx là tia phân giác của góc ngoài tại đỉnh C. CM Cx//AB
Cho Δ ABC có góc B + góc C = 60 độ. Trên đường phân giác AB của góc A lấy điểm I. Trên tia đối của tia AB lấy điểm F sao cho AF = AI. Trên tia đối của tia AC lấy E sao cho AE = AI. Chứng mình: a) AB và AC lần lượt là các đường trung trực của IE và IF; b) ΔIEF là Δ đều; c) IA ⊥ EF
Bài 3. (3,0 điểm) Cho tam giác ABC, lấy M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD.
a) Chứng minh AMB = DMC;
b) Chứng minh AC // BD;
c) Kẻ AH ⊥ BC, DK ⊥ BC (H, K thuộc BC). Chứng minh BK = CH;
d) Gọi I là trung điểm của AC, vẽ điểm E sao cho I là trung điểm của BE. Chứng minh C là trung điểm của DE.
Cho tam giác ABC vuông tại A có , đường cao AH. Trên tia đối của tia HB lấy điểm M sao cho HM = HB.
a) Chứng minh rằng HB < HC.
b) Chứng minh rằng AHB = AHM. Từ đó suy ra ABM là tam giác đều.
c) Gọi N là trung điểm của AC và O là giao điểm của AM và BN. Biết AB = 4 cm, tính độ dài đoạn thẳng AO.
Bài 2 : Cho tam giác ABC cân tại A ( A nhọn ) . Tia phân giác góc của A cắt BC tại I
a) C/m AI vuông góc BC
b) Gọi D là trung điểm của AC , M là giao điểm của BD với AI . C/m M là trọng tâm của tam giác ABC
c) Biết AB=AC=5cm;BC=6cm.Tím AM