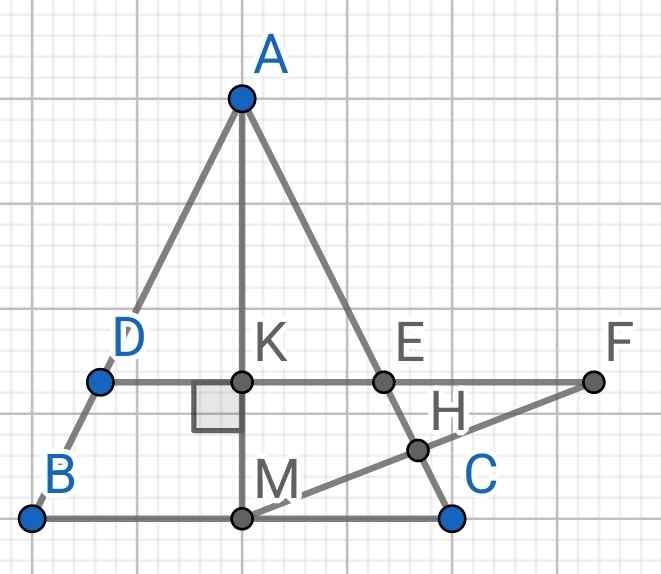
Cho tam giác ABC có AB = AC, M là trung điểm của BC. a) Chứng minh tam giác AMB = tam giác AMC. b) Trên cạnh AB lấy điểm D. Từ D kẻ đường vuông góc với AM tại K và kéo dài cắt cạnh AC tại E. Chứng minh tam giác ADE cân. c) Trên tia đối của tia ED lấy điểm F sao cho EF = MC, gọi H là trung điểm của EC. Chứng minh ba điểm M, H, F thẳng hàng.
 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ BM = CM
Xét ∆AMB và ∆AMC có:
AM là cạnh chung
AB = AC (gt)
BM = CM (cmt)
⇒ ∆AMB = ∆AMC (c-c-c)
b) Do ∆AMB = ∆AMC (cmt)
⇒ ∠BAM = ∠CAM (hai góc tương ứng)
⇒ ∠DAK = ∠EAK
Xét hai tam giác vuông: ∆ADK và ∆AEK có:
AK là cạnh chung
∠DAK = ∠EAK (cmt)
⇒ ∆ADK = ∆AEK (cạnh góc vuông - góc nhọn kề)
⇒ AD = AE (hai cạnh tương ứng)
⇒ ∆ADE cân tại A
c) Do ∆AMB = ∆AMC (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
Mà DK ⊥ AM (gt)
⇒ DK // BC
⇒ EF // BC
⇒ ∠HEF = ∠HCM (so le trong)
Do H là trung điểm của EC (gt)
⇒ HE = HC
Xét ∆HEF và ∆HCM có:
HE = HC (cmt)
∠HEF = ∠HCM (cmt)
EF = CM (gt)
⇒ ∆HEF = ∆HCM (c-g-c)
⇒ ∠EHF = ∠CHM (hai góc tương ứng)
Mà ∠EHF + ∠CHF = 180⁰ (kề bù)
⇒ ∠CHM + ∠CHF = 180⁰
⇒ M, H, F thẳng hàng
a . Xét Δ A M B và Δ A M C có: A M là cạnh chung
M B = M C ( M là trung điểm B C )
A B = A C (gt)
⇒ Δ A M B = Δ A M C ( c . c . c )
b . Xét Δ A D K và Δ A E K có: A K là cạnh chung
ˆ B A M = ˆ C A M ( Δ A M B = Δ A M C )
ˆ A K D = ˆ A K E = 90
⇒ Δ A D K = Δ A E K ( g . c . g )
⇒ A D = A E (2 cạnh tương ứng) nên Δ A D E cân tại A
c . Vì Δ A M B = Δ A M C (cmt) ⇒ ˆ A M B = ˆ A M C (2 góc tương ứng) mà ˆ A M B + ˆ A M C = 180
⇒ ˆ A M B = ˆ A M C = 90
⇒ A M ⊥ B C
Lại có: D E ⊥ A M
⇒ D E / / B C
⇒ E F / / B C
suy ra ˆ E F C = ˆ E C M (so le trong) hay ˆ F E H = ˆ H C M
Xét Δ E F H và Δ C M H có: EH = HC (gt)
ˆ F E H = ˆ H C M (cmt)
E F = M C (gt)
⇒ Δ E F H = Δ C M H ( c . g . c )
⇒ ˆ E H F = ˆ C H M (2 góc tương ứng)
mà ˆ E H F + ˆ F H C = 180 (kề bù)
⇒ ˆ C H M + ˆ F H C = 180
⇒ ˆ F H M = 180
⇒ M , H , F thẳng hàng
Chúc bạn học tốt



