Xét ΔBEA và CDA, ta có:
BA = CA (giả thiết)
∠A chung
AE=AD (giả thiết)
Suy ra: ΔBEA = ΔCDA (c.g.c)
Vậy: BE = CD (hai cạnh tương ứng)

Xét ΔBEA và CDA, ta có:
BA = CA (giả thiết)
∠A chung
AE=AD (giả thiết)
Suy ra: ΔBEA = ΔCDA (c.g.c)
Vậy: BE = CD (hai cạnh tương ứng)
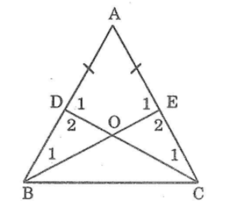
Cho tam giác ABC . Có AB = AC . Lấy điểm D trên cạnh AB . Lấy điểm E trên cạnh AC sao cho AD = AE a) Chứng minh BE = CD b) Gọi O là giao điểm của BE và CD . Chứng minh rằng tam giác BOD bằng tam giác COE
Cho tam giác ABC có AB = AC. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.
Gọi O là giao điểm của BE và CD
Chứng minh rằng ΔBOD=COE
cho tam giác ABC có AB=AC. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD=AE.
a) chứng minh BE=CD
b) gọi i là giao điểm của BE và CD. chứng minh rằng tam giác BID= CIE
cho tam giác ABC có AB =AC, lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho: AD = AE
a)Chứng minh rằng: BE=CD
b)Gọi O là giao điểm của BE và CD. Cứng minh: OB=OC
cho tam giác ABC có AB = AC . Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh rằng :
a, BE = CD
b, MDB = MEC
c, Am là p/g của góc BAC
Bài 2. Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên cạnh AC lấy điểm E sao cho AD = AE. a) Chứng minh rằng: BE = CD b) Chứng minh rằng: góc ABE bằng góc ACD c) Gọi K là giao điểm của BE và CD. Tam giác KBC là tam giác gì? Vì sao? d) Gọi I là trung điểm BC. Chứng minh A, K, I thẳng hàng
Cho tam giác ABC cân tại A, trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh rằng :
a) BE=CD
b)tam giác BMD = tam giác CME
Cho tam giác ABC có AB=AC. lấy điểm D trên cạnh AC, điểm E trên cạnh AC sao cho AD=AE.
CMR
a, BE=CD
b, Gọi O là giao điểm của BE và CD. Chứng minh tam giác BOD= tam giác COE
Cho tam giac ABC có AB=ACtreen cạnh AB lấy điểm D trên canh AC lấy điểm E sao cho AD=AE
a) chứng minh rằng BE=CD
b) gọi O là giao điểm của BE và CD chứng minh rằng tam giác BOD=tam giacCOE