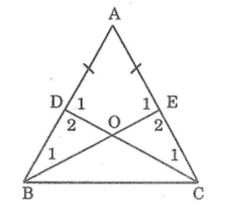
ΔBEA= ΔCDA (chứng minh trên)
⇒∠(B1 ) =∠(C1 ) ;∠(E1 ) =∠(D1 ) (hai góc tương ứng) (1)
+) Ta có: ∠(E1 ) +∠(E2 ) =180o (hai góc kề bù) (2)
Và ∠(D1 ) +∠(D2 ) =180o (hai góc kề bù) (3)
Từ (1); (2) và (3) suy ra: ∠(E2 ) =∠(D2 )
+) Theo giả thiết ta có; AB = AC
Và AD = AE
Lấy vế trừ vế, suy ra:
AB - AD = AC - AE hay BD = CE
Xét ΔOEC và ΔOCE, ta có:
∠(D2 ) =∠(E2 ) (chứng minh trên)
DB=EC (chứng minh trên)
∠(B1 ) =∠(C1 ) (chứng minh trên)
Suy ra: ΔODB= ΔOCE ( g.c.g)

