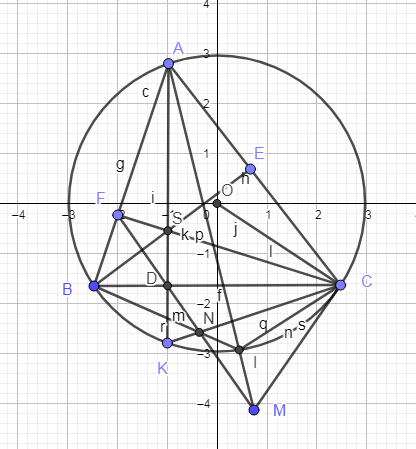
Cho tam giác ABC có 3 góc nhọn, AB < AC và nội tiếp đường tròn (O). Ba đường cao AD, BE, CF cắt nhau tại H. Tia AD cắt đường tròn (O) ở K( K khác A). Tiếp tuyến tại C của đường tròn (O) cắt đường thẳng FD tại M. AM cắt đường tròn (O) tại I( I khác A). MD cắt BI tại N. Chứng minh 3 điểm C, K, N thẳng hàng.
MC^2=MI*MA=MD^2
=>MD/MA=MI/MD
=>ΔMDI đồng dạng với ΔMAD
DNIC nội tiếp
=>góc NDI=góc NCI
=>góc MCI=góc NAD
=>góc NCI=góc KCI
=>C,K,N thẳng hàng