Question

Cho tam giác ABC cân tại A . Trên cạnh AB,AC lần lượt lấy các điểm K,H sao cho AK=AH.GỌI O là giao điểm của BH và CK.Chứng minh tam giác OCB cân. (kèm theo hình ạ)
Mình đang cần gấp bạn nào giải nhanh,đúng thì mình tick cho ạ

Answer 1

  

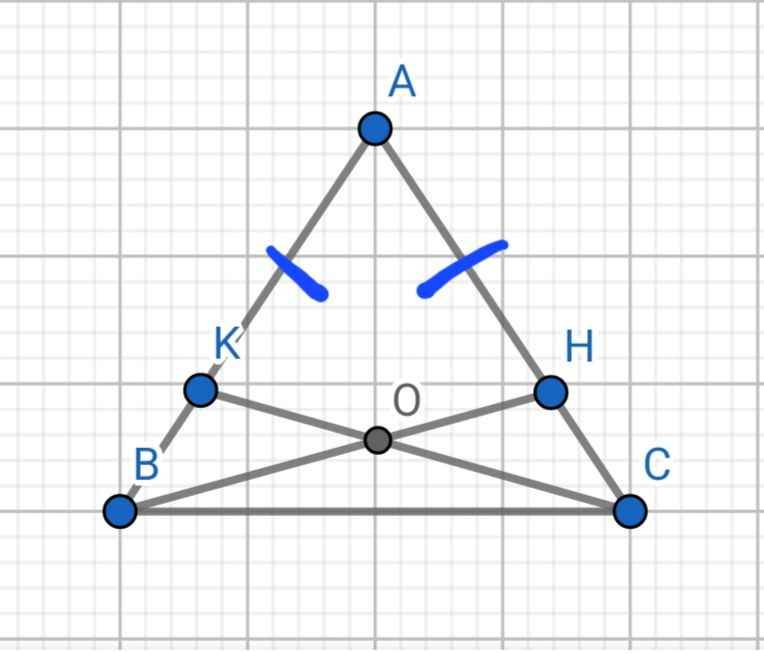
Do ∆ABC cân tại A

⇒ AB = AC và ∠ABC = ∠ACB

AK = AH

⇒ BK = CH

Xét ∆BHC và ∆CKB có:

CH = BK (cmt)

∠BCH = ∠CBK (∠ACB = ∠ABC)

BC chung

⇒ ∆BHC = ∆CKB (c-g-c)

⇒ ∠HBC = ∠KCB (hai góc tương ứng)

∠OBC = ∠OCB

∆OBC có ∠OBC = ∠OCB

⇒ ∆OBC cân tại O