Đáp án cần chọn là: B
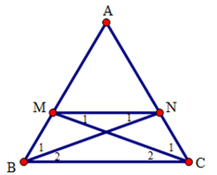
Ta có AB = AM + MB và AC = AN + NC
Mà AB = AC (do tam giác ABC cân tại A) và BM = NC (gt)
Suy ra AN = AM
Xét tam giác AMN cân tại A.
Suy ra A M N ^ = A N M ^ .
Xét tam giác ANM có: A ^ + A M N ^ + A N M ^ (tổng ba góc trong một tam giác)
A M N ^ = 180 0 − A 2 (vì A M N ^ = A N M ^ ) (1)
Xét tam giác ABC cân tại A ta có:
A ^ + B ^ + C ^ = 180 ° (tổng ba góc trong một tam giác) nên B ^ = 180 0 − A 2 (vì B ^ = C ^ ) (2)
Từ (1) và (2) A M N ^ = B ^
Mà B ^ , A M N ^ là hai góc đồng vị nên MN // BC
Xét tứ giác MNCB có MN // BC nên MNCB là hình thang.
Lại có B ^ = C ^ (do ΔABC cân tại A) nên MNCB là hình thang cân.

