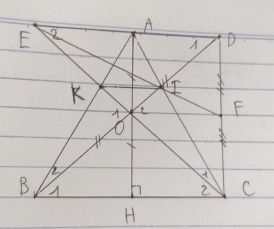
Cho tam giác ABC cân tại A có đường cao AH và O là trung điểm của AH. Trên tia đối của tia OB lấy điểm D sao cho OD = OB
a, Chứng minh tam giác OBH = tam giác ODA và AH vuông góc với AD
b, Tia CO cắt đường thẳng AD tại E. Chứng minh A là trung điểm của đoạn thẳng DE.
c, AC cắt BD tại I và gọi F là trung điểm của DC, Chứng minh 3 điểm E, I, F thẳng hàng
d, AB cắt CE tại K. Chứng minh IK song song với ED
a) Xét ΔOBH và ΔODA có
OB=OD(gt)
\(\widehat{BOH}=\widehat{DOA}\)(hai góc đối đỉnh)
OH=OA(gt)
Do đó: ΔOBH=ΔODA(c-g-c)
Suy ra: \(\widehat{OHB}=\widehat{OAD}\)(hai góc tương ứng)
mà \(\widehat{OHB}=90^0\)(gt)
nên \(\widehat{OAD}=90^0\)
hay AH\(\perp\)AD(đpcm)
b) Xét ΔAOE vuông tại A và ΔHOC vuông tại H có
OA=OH(O là trung điểm của AH)
\(\widehat{AOE}=\widehat{HOC}\)(hai góc đối đỉnh)
Do đó: ΔAOE=ΔHOC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AE=HC(Hai cạnh tương ứng)(1)
Ta có: ΔAOD=ΔHOB(cmt)
nên AD=HB(Hai cạnh tương ứng)(2)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔBAC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(Cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(Hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra AE=AD
mà A nằm giữa D và E
nên A là trung điểm của DE