Question

Cho tam giác ABC cân tại A có AB=34cm,BC=32cm.Kẻ đường trung tuyến AM.

A)chứng minh AM vuông góc BC.

B)tính AM

Answer 1

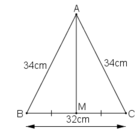
a.Ta có: AM là đường trung tuyến trong tam giác cân ABC 

=> Cũng là đường cao

=> AM vuông góc với BC

b.Có AM là đường trung tuyến \(\Rightarrow BM=BC:2=32:2=16cm\)

Áp dụng định lý pytago vào tam giác vuông ABM, có:

\(AB^2=AM^2+BM^2\)

\(\Rightarrow AM^2=34^2-16^2\)

\(AM=\sqrt{900}=30cm\)

 

Answer 2

\(a)\text{Xét }\Delta ACM\text{ và }\Delta ABM\text{ có:}\)

\(AB=AC\left(\Delta ABC\text{ cân tại A}\right)\)

\(\widehat{B}=\widehat{C}\left(\Delta ABC\text{ cân tại A}\right)\)

\(AM\text{ chung}\)

\(\Rightarrow\Delta ACM=\Delta ABM\left(c-g-c\right)\)

\(\Rightarrow\widehat{AMC}=\widehat{AMB}\left(\text{hai góc tương ứng}\right)\)

\(\text{Mà chúng kề bù}\)

\(\Rightarrow\widehat{AMC}=\widehat{AMB}=\dfrac{180^0}{2}=90^0\)

\(\Rightarrow AM\perp BC\)

\(b)\text{Ta có:}\Delta ACM=\Delta ABM\left(cmt\right)\)

\(\Rightarrow CM=BM\left(\text{hai cạnh tương ứng}\right)\)

\(\Rightarrow CM=BM=\dfrac{BC}{2}=\dfrac{32}{2}=16\left(cm\right)\)

\(\text{Xét }\Delta AMB\text{ vuông tại M có:}\)

\(AB^2=AM^2+BM^2\)

\(\Rightarrow AM^2=AB^2-BM^2\left(\text{định lý Py ta go}\right)\)

\(\Rightarrow AM^2=34^2-16^2=1156-256=900\)

\(\Rightarrow AM=\sqrt{900}=30\left(cm\right)\)