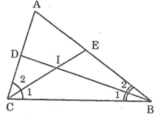
∠B = 80o, ∠C = 40o
Ta có:
∠(B1) = (1/2)∠(ABC) = (1/2).80o = 40o (vì BD là tia phân giác ∠(ABC))
∠(C1) = (1/2)∠(ACB) = (1/2).40o = 20o (vì CE là tia phân giác ∠(ACB))
Trong ΔIBC, ta có: ∠(BIC) + ∠(B1) + ∠(C1) = 180o(tổng 3 góc trong tam giác)
Vậy: ∠(BIC) = 180o - (∠(B1) + ∠(C1)) = 180o - (40o + 20o) = 120o

