`\color {blue} \text {_Namm_}`
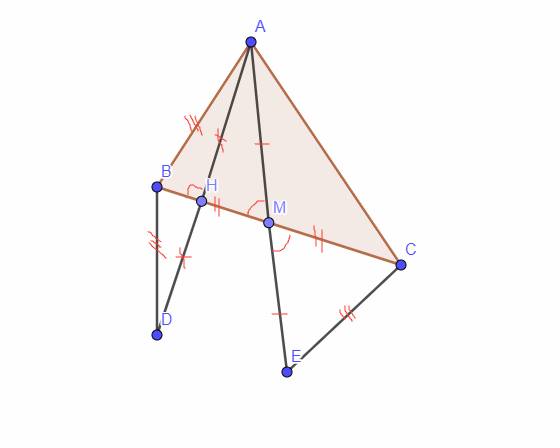
Mình xp sửa đề: Cho Tam giác `ABC (AB<AC)` (chứ nếu để vậy sẽ bị sai lệch thông tin của hình ;-;;)
`a,` Xét Tam giác `AMB` và Tam giác `CME` có:
`AM = EM (g``t)`
\(\widehat{AMB}=\widehat{CME}\) `(2` góc đối đỉnh `)`
`MB=MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `CME (c-g-c)`
`b,` Vì Tam giác `AMB =` Tam giác `CME (a)`
`-> AB=CE (2` cạnh tương ứng `)`
Xét Tam giác `ABH` và Tam giác `DBH` có:
`HA = HD (g``t)`
\(\widehat{AHB}=\widehat{DHB}=90^0\)
`BH` chung
`=>` Tam giác `ABH =` Tam giác `DBH (c-g-c)`
`-> AB=BD (2` cạnh tương ứng `)`
Mà `AB = CE -> BD=CE`