Chọn D.
Ta có: sin2α = a ⇒ 2sinα.cosα = a với 0 < α < 90o.
sin 2 α + cos 2 α = 1
⇔ sin 2 α + cos 2 α + 2sinαcosα - 2sinαcosα = 1
⇔ (sinα + cosα ) 2 - 2sinαcosα = 1
⇔ (sinα + cosα ) 2 = 1 + 2sinαcosα
⇔ (sinα + cosα ) 2 = 1 + a

Chọn D.
Ta có: sin2α = a ⇒ 2sinα.cosα = a với 0 < α < 90o.
sin 2 α + cos 2 α = 1
⇔ sin 2 α + cos 2 α + 2sinαcosα - 2sinαcosα = 1
⇔ (sinα + cosα ) 2 - 2sinαcosα = 1
⇔ (sinα + cosα ) 2 = 1 + 2sinαcosα
⇔ (sinα + cosα ) 2 = 1 + a

Cho góc α thỏa mãn π 2 < α < π . Biết sinα + 2cosα = -1, giá trị của sin2α là:
A. 2 6 5
B. 24 25
C. - 2 6 5
D. - 24 25
Trong các hệ thức sau, hệ thức nào không đúng ?
(A) (sin α+cos α)^2=1+2sin α cos α;
(B) (sinα−cosα)2=1−2sinαcosα(sinα−cosα)2=1−2sinαcosα;
(C) cos^4α−sin^4α=cos^2α−sin^2α;
(D) cos^4α+sin^4α=1.
Cho góc α thỏa mãn π 2 < α < π và sinα + 2cosα = -1. Giá trị sin2α là:
A. 2 6 5
B. 24 25
C. - 2 6 5
D. - 24 25
Với tan α = - 4 5 v ớ i 3 π 2 < α < 2 π . Giá trị của sinα và cosα là:
A. sin α = - 4 41 , cos α = - 5 41
B. sin α = 4 41 , cos α = 5 41
C. sin α = - 4 41 , cos α = 5 41
D. sin α = 4 41 , cos α = - 5 41
Cho sinα = -2 5 /5 với 3π/2 < α < 2π. Giá trị cotα là
A. 1/2 B. 1/ 5
C. -1/2 D. -3/ 5
Cho các số thực a. b, c, d thỏa mãn a^2 + b^2 - 2a +4b + 1 = 0 và 2c - d + 1 = 0. tìm giá trị nhỏ nhất của biêu thức P= (a-c)^2 + (b-d)^2
Cho các hàm số
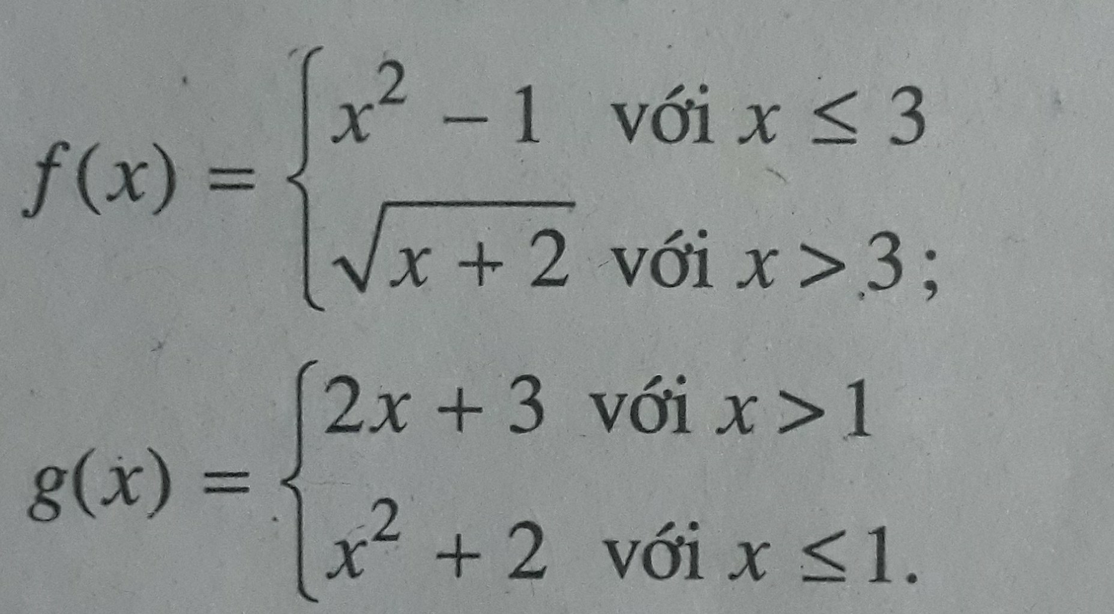
Khi đó giá trị: f(0) + 2f(7) - g(1) bằng:
A. 2 B. 0 C. 2 + 3 D. -2
Với giá trị nào của a thì hai bất phương trình sau đây tương đương?
(a-1) x- a+ 3> 0 (1)
(a+1) x-a+2> 0 (2)
A. a = 1
B. a = 5
C. a = - 1
D. -1 < a < 1
Biết sina = -4/5 với 3π/4 < a < π. Giá trị tan a là
A. 1/2 B. 2
C. -2 D. -1/2